Author: Jason Brownlee
Generative adversarial networks, or GANs, are effective at generating high-quality synthetic images.
A limitation of GANs is that the are only capable of generating relatively small images, such as 64×64 pixels.
The Progressive Growing GAN is an extension to the GAN training procedure that involves training a GAN to generate very small images, such as 4×4, and incrementally increasing the size of the generated images to 8×8, 16×16, until the desired output size is met. This has allowed the progressive GAN to generate photorealistic synthetic faces with 1024×1024 pixel resolution.
The key innovation of the progressive growing GAN is the two-phase training procedure that involves the fading-in of new blocks to support higher-resolution images followed by fine-tuning.
In this tutorial, you will discover how to implement and train a progressive growing generative adversarial network for generating celebrity faces.
After completing this tutorial, you will know:
- How to prepare the celebrity faces dataset for training a progressive growing GAN model.
- How to define and train the progressive growing GAN on the celebrity faces dataset.
- How to load saved generator models and use them for generating ad hoc synthetic celebrity faces.
Discover how to develop DCGANs, conditional GANs, Pix2Pix, CycleGANs, and more with Keras in my new GANs book, with 29 step-by-step tutorials and full source code.
Let’s get started.

How to Train a Progressive Growing GAN in Keras for Synthesizing Faces.
Photo by Alessandro Caproni, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
- What Is the Progressive Growing GAN
- How to Prepare the Celebrity Faces Dataset
- How to Develop Progressive Growing GAN Models
- How to Train Progressive Growing GAN Models
- How to Synthesize Images With a Progressive Growing GAN Model
What Is the Progressive Growing GAN
GANs are effective at generating crisp synthetic images, although are typically limited in the size of the images that can be generated.
The Progressive Growing GAN is an extension to the GAN that allows the training generator models to be capable of generating large high-quality images, such as photorealistic faces with the size 1024×1024 pixels. It was described in the 2017 paper by Tero Karras, et al. from Nvidia titled “Progressive Growing of GANs for Improved Quality, Stability, and Variation.”
The key innovation of the Progressive Growing GAN is the incremental increase in the size of images output by the generator, starting with a 4×4 pixel image and doubling to 8×8, 16×16, and so on until the desired output resolution.
This is achieved by a training procedure that involves periods of fine-tuning the model with a given output resolution, and periods of slowly phasing in a new model with a larger resolution. All layers remain trainable during the training process, including existing layers when new layers are added.
Progressive Growing GAN involves using a generator and discriminator model with the same general structure and starting with very small images. During training, new blocks of convolutional layers are systematically added to both the generator model and the discriminator models.
The incremental addition of the layers allows the models to effectively learn coarse-level detail and later learn ever-finer detail, both on the generator and discriminator sides.
This incremental nature allows the training to first discover large-scale structure of the image distribution and then shift attention to increasingly finer-scale detail, instead of having to learn all scales simultaneously.
The next step is to select a dataset to use for developing a Progressive Growing GAN.
Want to Develop GANs from Scratch?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
How to Prepare the Celebrity Faces Dataset
In this tutorial, we will use the Large-scale Celebrity Faces Attributes Dataset, referred to as CelebA.
This dataset was developed and published by Ziwei Liu, et al. for their 2015 paper tilted “From Facial Parts Responses to Face Detection: A Deep Learning Approach.”
The dataset provides about 200,000 photographs of celebrity faces along with annotations for what appears in given photos, such as glasses, face shape, hats, hair type, etc. As part of the dataset, the authors provide a version of each photo centered on the face and cropped to the portrait with varying sizes around 150 pixels wide and 200 pixels tall. We will use this as the basis for developing our GAN model.
The dataset can be easily downloaded from the Kaggle webpage. Note: this may require an account with Kaggle.
Specifically, download the file “img_align_celeba.zip“, which is about 1.3 gigabytes. To do this, click on the filename on the Kaggle website and then click the download icon.
The download might take a while depending on the speed of your internet connection.
After downloading, unzip the archive.
This will create a new directory named “img_align_celeba” that contains all of the images with filenames like 202599.jpg and 202598.jpg.
When working with a GAN, it is easier to model a dataset if all of the images are small and square in shape.
Further, as we are only interested in the face in each photo and not the background, we can perform face detection and extract only the face before resizing the result to a fixed size.
There are many ways to perform face detection. In this case, we will use a pre-trained Multi-Task Cascaded Convolutional Neural Network, or MTCNN. This is a state-of-the-art deep learning model for face detection, described in the 2016 paper titled “Joint Face Detection and Alignment Using Multitask Cascaded Convolutional Networks.”
We will use the implementation provided by Iván de Paz Centeno in the ipazc/mtcnn project. This can also be installed via pip as follows:
sudo pip install mtcnn
We can confirm that the library was installed correctly by importing the library and printing the version; for example:
# confirm mtcnn was installed correctly import mtcnn # print version print(mtcnn.__version__)
Running the example prints the current version of the library.
0.0.8
The MTCNN model is very easy to use.
First, an instance of the MTCNN model is created, then the detect_faces() function can be called passing in the pixel data for one image.
The result a list of detected faces, with a bounding box defined in pixel offset values.
... # prepare model model = MTCNN() # detect face in the image faces = model.detect_faces(pixels) # extract details of the face x1, y1, width, height = faces[0]['box']
Although the progressive growing GAN supports the synthesis of large images, such as 1024×1024, this requires enormous resources, such as a single top of the line GPU training the model for a month.
Instead, we will reduce the size of the generated images to 128×128 which will, in turn, allow us to train a reasonable model on a GPU in a few hours and still discover how the progressive growing model can be implemented, trained, and used.
As such, we can develop a function to load a file and extract the face from the photo, then and resize the extracted face pixels to a predefined size. In this case, we will use the square shape of 128×128 pixels.
The load_image() function below will load a given photo file name as a NumPy array of pixels.
# load an image as an rgb numpy array
def load_image(filename):
# load image from file
image = Image.open(filename)
# convert to RGB, if needed
image = image.convert('RGB')
# convert to array
pixels = asarray(image)
return pixels
The extract_face() function below takes the MTCNN model and pixel values for a single photograph as arguments and returns a 128x128x3 array of pixel values with just the face, or None if no face was detected (which can happen rarely).
# extract the face from a loaded image and resize def extract_face(model, pixels, required_size=(128, 128)): # detect face in the image faces = model.detect_faces(pixels) # skip cases where we could not detect a face if len(faces) == 0: return None # extract details of the face x1, y1, width, height = faces[0]['box'] # force detected pixel values to be positive (bug fix) x1, y1 = abs(x1), abs(y1) # convert into coordinates x2, y2 = x1 + width, y1 + height # retrieve face pixels face_pixels = pixels[y1:y2, x1:x2] # resize pixels to the model size image = Image.fromarray(face_pixels) image = image.resize(required_size) face_array = asarray(image) return face_array
The load_faces() function below enumerates all photograph files in a directory and extracts and resizes the face from each and returns a NumPy array of faces.
We limit the total number of faces loaded via the n_faces argument, as we don’t need them all.
# load images and extract faces for all images in a directory def load_faces(directory, n_faces): # prepare model model = MTCNN() faces = list() # enumerate files for filename in listdir(directory): # load the image pixels = load_image(directory + filename) # get face face = extract_face(model, pixels) if face is None: continue # store faces.append(face) print(len(faces), face.shape) # stop once we have enough if len(faces) >= n_faces: break return asarray(faces)
Tying this together, the complete example of preparing a dataset of celebrity faces for training a GAN model is listed below.
In this case, we increase the total number of loaded faces to 50,000 to provide a good training dataset for our GAN model.
# example of extracting and resizing faces into a new dataset
from os import listdir
from numpy import asarray
from numpy import savez_compressed
from PIL import Image
from mtcnn.mtcnn import MTCNN
from matplotlib import pyplot
# load an image as an rgb numpy array
def load_image(filename):
# load image from file
image = Image.open(filename)
# convert to RGB, if needed
image = image.convert('RGB')
# convert to array
pixels = asarray(image)
return pixels
# extract the face from a loaded image and resize
def extract_face(model, pixels, required_size=(128, 128)):
# detect face in the image
faces = model.detect_faces(pixels)
# skip cases where we could not detect a face
if len(faces) == 0:
return None
# extract details of the face
x1, y1, width, height = faces[0]['box']
# force detected pixel values to be positive (bug fix)
x1, y1 = abs(x1), abs(y1)
# convert into coordinates
x2, y2 = x1 + width, y1 + height
# retrieve face pixels
face_pixels = pixels[y1:y2, x1:x2]
# resize pixels to the model size
image = Image.fromarray(face_pixels)
image = image.resize(required_size)
face_array = asarray(image)
return face_array
# load images and extract faces for all images in a directory
def load_faces(directory, n_faces):
# prepare model
model = MTCNN()
faces = list()
# enumerate files
for filename in listdir(directory):
# load the image
pixels = load_image(directory + filename)
# get face
face = extract_face(model, pixels)
if face is None:
continue
# store
faces.append(face)
print(len(faces), face.shape)
# stop once we have enough
if len(faces) >= n_faces:
break
return asarray(faces)
# directory that contains all images
directory = 'img_align_celeba/'
# load and extract all faces
all_faces = load_faces(directory, 50000)
print('Loaded: ', all_faces.shape)
# save in compressed format
savez_compressed('img_align_celeba_128.npz', all_faces)
Running the example may take a few minutes given the larger number of faces to be loaded.
At the end of the run, the array of extracted and resized faces is saved as a compressed NumPy array with the filename ‘img_align_celeba_128.npz‘.
The prepared dataset can then be loaded any time, as follows.
# load the prepared dataset
from numpy import load
# load the face dataset
data = load('img_align_celeba_128.npz')
faces = data['arr_0']
print('Loaded: ', faces.shape)
Loading the dataset summarizes the shape of the array, showing 50K images with the size of 128×128 pixels and three color channels.
Loaded: (50000, 128, 128, 3)
We can elaborate on this example and plot the first 100 faces in the dataset as a 10×10 grid. The complete example is listed below.
# load the prepared dataset
from numpy import load
from matplotlib import pyplot
# plot a list of loaded faces
def plot_faces(faces, n):
for i in range(n * n):
# define subplot
pyplot.subplot(n, n, 1 + i)
# turn off axis
pyplot.axis('off')
# plot raw pixel data
pyplot.imshow(faces[i].astype('uint8'))
pyplot.show()
# load the face dataset
data = load('img_align_celeba_128.npz')
faces = data['arr_0']
print('Loaded: ', faces.shape)
plot_faces(faces, 10)
Running the example loads the dataset and creates a plot of the first 100 images.
We can see that each image only contains the face and all faces have the same square shape. Our goal is to generate new faces with the same general properties.
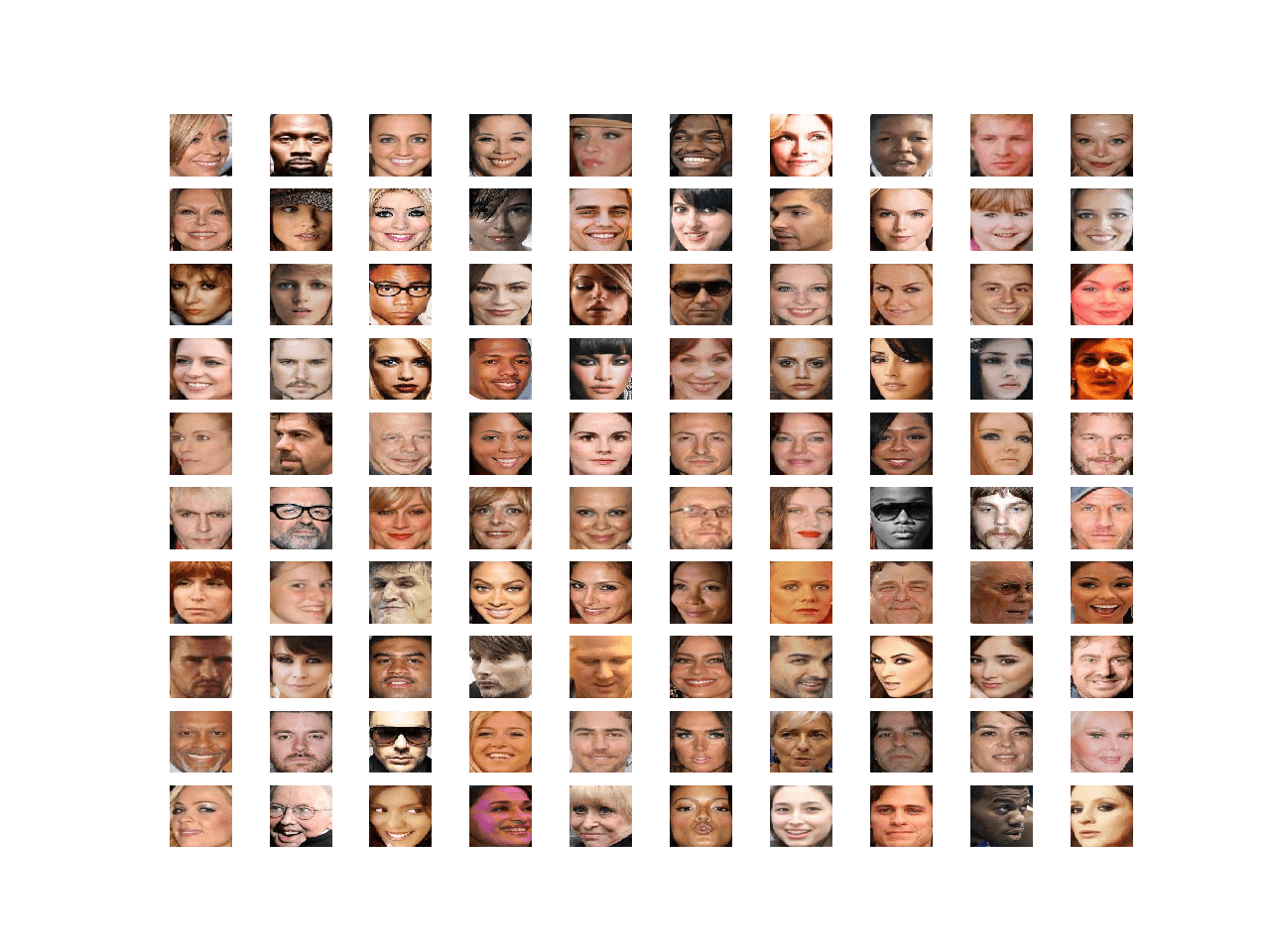
Plot of 100 Celebrity Faces in a 10×10 Grid
We are now ready to develop a GAN model to generate faces using this dataset.
How to Develop Progressive Growing GAN Models
There are many ways to implement the progressive growing GAN models.
In this tutorial, we will develop and implement each phase of growth as a separate Keras model and each model will share the same layers and weights.
This approach allows for the convenient training of each model, just like a normal Keras model, although it requires a slightly complicated model construction process to ensure that the layers are reused correctly.
First, we will define some custom layers required in the definition of the generator and discriminator models, then proceed to define functions to create and grow the discriminator and generator models themselves.
Progressive Growing Custom Layers
There are three custom layers required to implement the progressive growing generative adversarial network.
They are the layers:
- WeightedSum: Used to control the weighted sum of the old and new layers during a growth phase.
- MinibatchStdev: Used to summarize statistics for a batch of images in the discriminator.
- PixelNormalization: Used to normalize activation maps in the generator model.
Additionally, a weight constraint is used in the paper referred to as “equalized learning rate“. This too would need to be implemented as a custom layer. In the interest of brevity, we won’t use equalized learning rate in this tutorial and instead we use a simple max norm weight constraint.
WeightedSum Layer
The WeightedSum layer is a merge layer that combines the activations from two input layers, such as two input paths in a discriminator or two output paths in a generator model. It uses a variable called alpha that controls how much to weight the first and second inputs.
It is used during the growth phase of training when the model is in transition from one image size to a new image size with double the width and height (quadruple the area), such as from 4×4 to 8×8 pixels.
During the growth phase, the alpha parameter is linearly scaled from 0.0 at the beginning to 1.0 at the end, allowing the output of the layer to transition from giving full weight to the old layers to giving full weight to the new layers (second input).
- weighted sum = ((1.0 – alpha) * input1) + (alpha * input2)
The WeightedSum class is defined below as an extension to the Add merge layer.
# weighted sum output class WeightedSum(Add): # init with default value def __init__(self, alpha=0.0, **kwargs): super(WeightedSum, self).__init__(**kwargs) self.alpha = backend.variable(alpha, name='ws_alpha') # output a weighted sum of inputs def _merge_function(self, inputs): # only supports a weighted sum of two inputs assert (len(inputs) == 2) # ((1-a) * input1) + (a * input2) output = ((1.0 - self.alpha) * inputs[0]) + (self.alpha * inputs[1]) return output
MinibatchStdev
The mini-batch standard deviation layer, or MinibatchStdev, is only used in the output block of the discriminator layer.
The objective of the layer is to provide a statistical summary of the batch of activations. The discriminator can then learn to better detect batches of fake samples from batches of real samples. This, in turn, encourages the generator that is trained via the discriminator to create batches of samples with realistic batch statistics.
It is implemented as calculating the standard deviation for each pixel value in the activation maps across the batch, calculating the average of this value, and then creating a new activation map (one channel) that is appended to the list of activation maps provided as input.
The MinibatchStdev layer is defined below.
# mini-batch standard deviation layer class MinibatchStdev(Layer): # initialize the layer def __init__(self, **kwargs): super(MinibatchStdev, self).__init__(**kwargs) # perform the operation def call(self, inputs): # calculate the mean value for each pixel across channels mean = backend.mean(inputs, axis=0, keepdims=True) # calculate the squared differences between pixel values and mean squ_diffs = backend.square(inputs - mean) # calculate the average of the squared differences (variance) mean_sq_diff = backend.mean(squ_diffs, axis=0, keepdims=True) # add a small value to avoid a blow-up when we calculate stdev mean_sq_diff += 1e-8 # square root of the variance (stdev) stdev = backend.sqrt(mean_sq_diff) # calculate the mean standard deviation across each pixel coord mean_pix = backend.mean(stdev, keepdims=True) # scale this up to be the size of one input feature map for each sample shape = backend.shape(inputs) output = backend.tile(mean_pix, (shape[0], shape[1], shape[2], 1)) # concatenate with the output combined = backend.concatenate([inputs, output], axis=-1) return combined # define the output shape of the layer def compute_output_shape(self, input_shape): # create a copy of the input shape as a list input_shape = list(input_shape) # add one to the channel dimension (assume channels-last) input_shape[-1] += 1 # convert list to a tuple return tuple(input_shape)
PixelNormalization
The generator and discriminator models don’t use batch normalization like other GAN models; instead, each pixel in the activation maps is normalized to unit length.
This is a variation of local response normalization and is referred to in the paper as pixelwise feature vector normalization. Also, unlike other GAN models, normalization is only used in the generator model, not the discriminator.
This is a type of activity regularization and could be implemented as an activity constraint, although it is easily implemented as a new layer that scales the activations of the prior layer.
The PixelNormalization class below implements this and can be used after each Convolution layer in the generator, but before any activation function.
# pixel-wise feature vector normalization layer class PixelNormalization(Layer): # initialize the layer def __init__(self, **kwargs): super(PixelNormalization, self).__init__(**kwargs) # perform the operation def call(self, inputs): # calculate square pixel values values = inputs**2.0 # calculate the mean pixel values mean_values = backend.mean(values, axis=-1, keepdims=True) # ensure the mean is not zero mean_values += 1.0e-8 # calculate the sqrt of the mean squared value (L2 norm) l2 = backend.sqrt(mean_values) # normalize values by the l2 norm normalized = inputs / l2 return normalized # define the output shape of the layer def compute_output_shape(self, input_shape): return input_shape
We now have all of the custom layers required and can define our models.
Progressive Growing Discriminator Model
The discriminator model is defined as a deep convolutional neural network that expects a 4×4 color image as input and predicts whether it is real or fake.
The first hidden layer is a 1×1 convolutional layer. The output block involves a MinibatchStdev, 3×3, and 4×4 convolutional layers, and a fully connected layer that outputs a prediction. Leaky ReLU activation functions are used after all layers and the output layers use a linear activation function.
This model is trained for normal interval then the model undergoes a growth phase to 8×8. This involves adding a block of two 3×3 convolutional layers and an average pooling downsample layer. The input image passes through the new block with a new 1×1 convolutional hidden layer. The input image is also passed through a downsample layer and through the old 1×1 convolutional hidden layer. The output of the old 1×1 convolution layer and the new block are then combined via a WeightedSum layer.
After an interval of training transitioning the WeightedSum’s alpha parameter from 0.0 (all old) to 1.0 (all new), another training phase is run to tune the new model with the old layer and pathway removed.
This process repeats until the desired image size is met, in our case, 128×128 pixel images.
We can achieve this with two functions: the define_discriminator() function that defines the base model that accepts 4×4 images and the add_discriminator_block() function that takes a model and creates a growth version of the model with two pathways and the WeightedSum and a second version of the model with the same layers/weights but without the old 1×1 layer and WeightedSum layers. The define_discriminator() function can then call the add_discriminator_block() function as many times as is needed to create the models up to the desired level of growth.
All layers are initialized with small Gaussian random numbers with a standard deviation of 0.02, which is common for GAN models. A maxnorm weight constraint is used with a value of 1.0, instead of the more elaborate ‘equalized learning rate‘ weight constraint used in the paper.
The paper defines a number of filters that increases with the depth of the model from 16 to 32, 64, all the way up to 512. This requires projection of the number of feature maps during the growth phase so that the weighted sum can be calculated correctly. To avoid this complication, we fix the number of filters to be the same in all layers.
Each model is compiled and will be fit. In this case, we will use Wasserstein loss (or WGAN loss) and the Adam version of stochastic gradient descent configured as is specified in the paper. The authors of the paper recommend exploring using both WGAN-GP loss and least squares loss and found that the former performed slightly better. Nevertheless, we will use Wasserstein loss as it greatly simplifies the implementation.
First, we must define the loss function as the average predicted value multiplied by the target value. The target value will be 1 for real images and -1 for fake images. This means that weight updates will seek to increase the divide between real and fake images.
# calculate wasserstein loss def wasserstein_loss(y_true, y_pred): return backend.mean(y_true * y_pred)
The functions for defining and creating the growth versions of the discriminator models are listed below.
We make careful use of the functional API and knowledge of the model structure to create the two models for each growth phase. The growth phase also always doubles the expected input shape.
# add a discriminator block def add_discriminator_block(old_model, n_input_layers=3): # weight initialization init = RandomNormal(stddev=0.02) # weight constraint const = max_norm(1.0) # get shape of existing model in_shape = list(old_model.input.shape) # define new input shape as double the size input_shape = (in_shape[-2].value*2, in_shape[-2].value*2, in_shape[-1].value) in_image = Input(shape=input_shape) # define new input processing layer d = Conv2D(128, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(in_image) d = LeakyReLU(alpha=0.2)(d) # define new block d = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(d) d = LeakyReLU(alpha=0.2)(d) d = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(d) d = LeakyReLU(alpha=0.2)(d) d = AveragePooling2D()(d) block_new = d # skip the input, 1x1 and activation for the old model for i in range(n_input_layers, len(old_model.layers)): d = old_model.layers[i](d) # define straight-through model model1 = Model(in_image, d) # compile model model1.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8)) # downsample the new larger image downsample = AveragePooling2D()(in_image) # connect old input processing to downsampled new input block_old = old_model.layers[1](downsample) block_old = old_model.layers[2](block_old) # fade in output of old model input layer with new input d = WeightedSum()([block_old, block_new]) # skip the input, 1x1 and activation for the old model for i in range(n_input_layers, len(old_model.layers)): d = old_model.layers[i](d) # define straight-through model model2 = Model(in_image, d) # compile model model2.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8)) return [model1, model2] # define the discriminator models for each image resolution def define_discriminator(n_blocks, input_shape=(4,4,3)): # weight initialization init = RandomNormal(stddev=0.02) # weight constraint const = max_norm(1.0) model_list = list() # base model input in_image = Input(shape=input_shape) # conv 1x1 d = Conv2D(128, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(in_image) d = LeakyReLU(alpha=0.2)(d) # conv 3x3 (output block) d = MinibatchStdev()(d) d = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(d) d = LeakyReLU(alpha=0.2)(d) # conv 4x4 d = Conv2D(128, (4,4), padding='same', kernel_initializer=init, kernel_constraint=const)(d) d = LeakyReLU(alpha=0.2)(d) # dense output layer d = Flatten()(d) out_class = Dense(1)(d) # define model model = Model(in_image, out_class) # compile model model.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8)) # store model model_list.append([model, model]) # create submodels for i in range(1, n_blocks): # get prior model without the fade-on old_model = model_list[i - 1][0] # create new model for next resolution models = add_discriminator_block(old_model) # store model model_list.append(models) return model_list
The define_discriminator() function is called by specifying the number of blocks to create.
We will create 6 blocks, which will create 6 pairs of models that expect the input image sizes of 4×4, 8×8, 16×16, 32×32, 64×64, 128×128.
The function returns a list where each element in the list contains two models. The first model is the ‘normal model‘ or straight through model, and the second is the version of the model that includes the old 1×1 and new block with the weighted sum, used for the transition or growth phase of training.
Progressive Growing Generator Model
The generator model takes a random point from the latent space as input and generates a synthetic image.
The generator models are defined in the same way as the discriminator models.
Specifically, a base model for generating 4×4 images is defined and growth versions of the model are created for the large image output size.
The main difference is that during the growth phase, the output of the model is the output of the WeightedSum layer. The growth phase version of the model involves first adding a nearest neighbor upsampling layer; this is then connected to the new block with the new output layer and to the old old output layer. The old and new output layers are then combined via a WeightedSum output layer.
The base model has an input block defined with a fully connected layer with a sufficient number of activations to create a given number of 4×4 feature maps. This is followed by 4×4 and 3×3 convolution layers and a 1×1 output layer that generates color images. New blocks are added with an upsample layer and two 3×3 convolutional layers.
The LeakyReLU activation function is used and the PixelNormalization layer is used after each convolutional layer. A linear activation function is used in the output layer, instead of the more common tanh function, yet real images are still scaled to the range [-1,1], which is common for most GAN models.
The paper defines the number of feature maps decreasing with the depth of the model from 512 to 16. As with the discriminator, the difference in the number of feature maps across blocks introduces a challenge for the WeightedSum, so for simplicity, we fix all layers to have the same number of filters.
Also like the discriminator model, weights are initialized with Gaussian random numbers with a standard deviation of 0.02 and the maxnorm weight constraint is used with a value of 1.0, instead of the equalized learning rate weight constraint used in the paper.
The functions for defining and growing the generator models are defined below.
# add a generator block def add_generator_block(old_model): # weight initialization init = RandomNormal(stddev=0.02) # weight constraint const = max_norm(1.0) # get the end of the last block block_end = old_model.layers[-2].output # upsample, and define new block upsampling = UpSampling2D()(block_end) g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(upsampling) g = PixelNormalization()(g) g = LeakyReLU(alpha=0.2)(g) g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(g) g = PixelNormalization()(g) g = LeakyReLU(alpha=0.2)(g) # add new output layer out_image = Conv2D(3, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(g) # define model model1 = Model(old_model.input, out_image) # get the output layer from old model out_old = old_model.layers[-1] # connect the upsampling to the old output layer out_image2 = out_old(upsampling) # define new output image as the weighted sum of the old and new models merged = WeightedSum()([out_image2, out_image]) # define model model2 = Model(old_model.input, merged) return [model1, model2] # define generator models def define_generator(latent_dim, n_blocks, in_dim=4): # weight initialization init = RandomNormal(stddev=0.02) # weight constraint const = max_norm(1.0) model_list = list() # base model latent input in_latent = Input(shape=(latent_dim,)) # linear scale up to activation maps g = Dense(128 * in_dim * in_dim, kernel_initializer=init, kernel_constraint=const)(in_latent) g = Reshape((in_dim, in_dim, 128))(g) # conv 4x4, input block g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(g) g = PixelNormalization()(g) g = LeakyReLU(alpha=0.2)(g) # conv 3x3 g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(g) g = PixelNormalization()(g) g = LeakyReLU(alpha=0.2)(g) # conv 1x1, output block out_image = Conv2D(3, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(g) # define model model = Model(in_latent, out_image) # store model model_list.append([model, model]) # create submodels for i in range(1, n_blocks): # get prior model without the fade-on old_model = model_list[i - 1][0] # create new model for next resolution models = add_generator_block(old_model) # store model model_list.append(models) return model_list
Calling the define_generator() function requires that the size of the latent space be defined.
Like the discriminator, we will set the n_blocks argument to 6 to create six pairs of models.
The function returns a list of models where each item in the list contains the normal or straight-through version of each generator and the growth version for phasing in the new block at the larger output image size.
Composite Models for Training the Generators
The generator models are not compiled as they are not trained directly.
Instead, the generator models are trained via the discriminator models using Wasserstein loss.
This involves presenting generated images to the discriminator as real images and calculating the loss that is then used to update the generator models.
A given generator model must be paired with a given discriminator model both in terms of the same image size (e.g. 4×4 or 8×8) and in terms of the same phase of training, such as growth phase (introducing the new block) or fine-tuning phase (normal or straight-through).
We can achieve this by creating a new model for each pair of models that stacks the generator on top of the discriminator so that the synthetic image feeds directly into the discriminator model to be deemed real or fake. This composite model can then be used to train the generator via the discriminator and the weights of the discriminator can be marked as not trainable (only in this model) to ensure they are not changed during this misleading process.
As such, we can create pairs of composite models, e.g. six pairs for the six levels of image growth, where each pair is comprised of a composite model for the normal or straight-through model, and the growth version of the model.
The define_composite() function implements this and is defined below.
# define composite models for training generators via discriminators def define_composite(discriminators, generators): model_list = list() # create composite models for i in range(len(discriminators)): g_models, d_models = generators[i], discriminators[i] # straight-through model d_models[0].trainable = False model1 = Sequential() model1.add(g_models[0]) model1.add(d_models[0]) model1.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8)) # fade-in model d_models[1].trainable = False model2 = Sequential() model2.add(g_models[1]) model2.add(d_models[1]) model2.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8)) # store model_list.append([model1, model2]) return model_list
Now that we have seen how to define the generator and discriminator models, let’s look at how we can fit these models on the celebrity faces dataset.
How to Train Progressive Growing GAN Models
First, we need to define some convenience functions for working with samples of data.
The load_real_samples() function below loads our prepared celebrity faces dataset, then converts the pixels to floating point values and scales them to the range [-1,1], common to most GAN implementations.
# load dataset
def load_real_samples(filename):
# load dataset
data = load(filename)
# extract numpy array
X = data['arr_0']
# convert from ints to floats
X = X.astype('float32')
# scale from [0,255] to [-1,1]
X = (X - 127.5) / 127.5
return X
Next, we need to be able to retrieve a random sample of images used to update the discriminator.
The generate_real_samples() function below implements this, returning a random sample of images from the loaded dataset and their corresponding target value of class=1 to indicate that the images are real.
# select real samples def generate_real_samples(dataset, n_samples): # choose random instances ix = randint(0, dataset.shape[0], n_samples) # select images X = dataset[ix] # generate class labels y = ones((n_samples, 1)) return X, y
Next, we need a sample of latent points used to create synthetic images with the generator model.
The generate_latent_points() function below implements this, returning a batch of latent points with the required dimensionality.
# generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network x_input = x_input.reshape(n_samples, latent_dim) return x_input
The latent points can be used as input to the generator to create a batch of synthetic images.
This is required to update the discriminator model. It is also required to update the generator model via the discriminator model with the composite models defined in the previous section.
The generate_fake_samples() function below takes a generator model and generates and returns a batch of synthetic images and the corresponding target for the discriminator of class=-1 to indicate that the images are fake. The generate_latent_points() function is called to create the required batch worth of random latent points.
# use the generator to generate n fake examples, with class labels def generate_fake_samples(generator, latent_dim, n_samples): # generate points in latent space x_input = generate_latent_points(latent_dim, n_samples) # predict outputs X = generator.predict(x_input) # create class labels y = -ones((n_samples, 1)) return X, y
Training the models occurs in two phases: a fade-in phase that involves the transition from a lower-resolution to a higher-resolution image, and the normal phase that involves the fine-tuning of the models at a given higher resolution image.
During the phase-in, the alpha value of the WeightedSum layers in the discriminator and generator model at a given level requires linear transition from 0.0 to 1.0 based on the training step. The update_fadein() function below implements this; given a list of models (such as the generator, discriminator, and composite model), the function locates the WeightedSum layer in each and sets the value for the alpha attribute based on the current training step number.
Importantly, this alpha attribute is not a constant but is instead defined as a changeable variable in the WeightedSum class and whose value can be changed using the Keras backend set_value() function.
This is a clumsy but effective approach to changing the alpha values. Perhaps a cleaner implementation would involve a Keras Callback and is left as an exercise for the reader.
# update the alpha value on each instance of WeightedSum def update_fadein(models, step, n_steps): # calculate current alpha (linear from 0 to 1) alpha = step / float(n_steps - 1) # update the alpha for each model for model in models: for layer in model.layers: if isinstance(layer, WeightedSum): backend.set_value(layer.alpha, alpha)
Next, we can define the procedure for training the models for a given training phase.
A training phase takes one generator, discriminator, and composite model and updates them on the dataset for a given number of training epochs. The training phase may be a fade-in transition to a higher resolution, in which case the update_fadein() must be called each iteration, or it may be a normal tuning training phase, in which case there are no WeightedSum layers present.
The train_epochs() function below implements the training of the discriminator and generator models for a single training phase.
A single training iteration involves first selecting a half batch of real images from the dataset and generating a half batch of fake images from the current state of the generator model. These samples are then used to update the discriminator model.
Next, the generator model is updated via the discriminator with the composite model, indicating that the generated images are, in fact, real, and updating generator weights in an effort to better fool the discriminator.
A summary of model performance is printed at the end of each training iteration, summarizing the loss of the discriminator on the real (d1) and fake (d2) images and the loss of the generator (g).
# train a generator and discriminator
def train_epochs(g_model, d_model, gan_model, dataset, n_epochs, n_batch, fadein=False):
# calculate the number of batches per training epoch
bat_per_epo = int(dataset.shape[0] / n_batch)
# calculate the number of training iterations
n_steps = bat_per_epo * n_epochs
# calculate the size of half a batch of samples
half_batch = int(n_batch / 2)
# manually enumerate epochs
for i in range(n_steps):
# update alpha for all WeightedSum layers when fading in new blocks
if fadein:
update_fadein([g_model, d_model, gan_model], i, n_steps)
# prepare real and fake samples
X_real, y_real = generate_real_samples(dataset, half_batch)
X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch)
# update discriminator model
d_loss1 = d_model.train_on_batch(X_real, y_real)
d_loss2 = d_model.train_on_batch(X_fake, y_fake)
# update the generator via the discriminator's error
z_input = generate_latent_points(latent_dim, n_batch)
y_real2 = ones((n_batch, 1))
g_loss = gan_model.train_on_batch(z_input, y_real2)
# summarize loss on this batch
print('>%d, d1=%.3f, d2=%.3f g=%.3f' % (i+1, d_loss1, d_loss2, g_loss))
Next, we need to call the train_epochs() function for each training phase.
This involves first scaling the training dataset to the required pixel dimensions, such as 4×4 or 8×8. The scale_dataset() function below implements this, taking the dataset and returning a scaled version.
These scaled versions of the dataset could be pre-computed and loaded instead of re-scaled on each run. This might be a nice extension if you intend to run the example many times.
# scale images to preferred size def scale_dataset(images, new_shape): images_list = list() for image in images: # resize with nearest neighbor interpolation new_image = resize(image, new_shape, 0) # store images_list.append(new_image) return asarray(images_list)
After each training run, we also need to save a plot of generated images and the current state of the generator model.
This is useful so that at the end of the run we can see the progression of the capability and quality of the model, and load and use a generator model at any point during the training process. A generator model could be used to create ad hoc images, or used as the starting point for continued training.
The summarize_performance() function below implements this, given a status string such as “faded” or “tuned“, a generator model, and the size of the latent space. The function will proceed to create a unique name for the state of the system using the “status” string such as “04×04-faded“, then create a plot of 25 generated images and save the plot and the generator model to file using the defined name.
# generate samples and save as a plot and save the model
def summarize_performance(status, g_model, latent_dim, n_samples=25):
# devise name
gen_shape = g_model.output_shape
name = '%03dx%03d-%s' % (gen_shape[1], gen_shape[2], status)
# generate images
X, _ = generate_fake_samples(g_model, latent_dim, n_samples)
# normalize pixel values to the range [0,1]
X = (X - X.min()) / (X.max() - X.min())
# plot real images
square = int(sqrt(n_samples))
for i in range(n_samples):
pyplot.subplot(square, square, 1 + i)
pyplot.axis('off')
pyplot.imshow(X[i])
# save plot to file
filename1 = 'plot_%s.png' % (name)
pyplot.savefig(filename1)
pyplot.close()
# save the generator model
filename2 = 'model_%s.h5' % (name)
g_model.save(filename2)
print('>Saved: %s and %s' % (filename1, filename2))
The train() function below pulls this together, taking the lists of defined models as input as well as the list of batch sizes and the number of training epochs for the normal and fade-in phases at each level of growth for the model.
The first generator and discriminator model for 4×4 images are fit by calling train_epochs() and saved by calling summarize_performance().
Then the steps of growth are enumerated, involving first scaling the image dataset to the preferred size, training and saving the fade-in model for the new image size, then training and saving the normal or fine-tuned model for the new image size.
# train the generator and discriminator
def train(g_models, d_models, gan_models, dataset, latent_dim, e_norm, e_fadein, n_batch):
# fit the baseline model
g_normal, d_normal, gan_normal = g_models[0][0], d_models[0][0], gan_models[0][0]
# scale dataset to appropriate size
gen_shape = g_normal.output_shape
scaled_data = scale_dataset(dataset, gen_shape[1:])
print('Scaled Data', scaled_data.shape)
# train normal or straight-through models
train_epochs(g_normal, d_normal, gan_normal, scaled_data, e_norm[0], n_batch[0])
summarize_performance('tuned', g_normal, latent_dim)
# process each level of growth
for i in range(1, len(g_models)):
# retrieve models for this level of growth
[g_normal, g_fadein] = g_models[i]
[d_normal, d_fadein] = d_models[i]
[gan_normal, gan_fadein] = gan_models[i]
# scale dataset to appropriate size
gen_shape = g_normal.output_shape
scaled_data = scale_dataset(dataset, gen_shape[1:])
print('Scaled Data', scaled_data.shape)
# train fade-in models for next level of growth
train_epochs(g_fadein, d_fadein, gan_fadein, scaled_data, e_fadein[i], n_batch[i], True)
summarize_performance('faded', g_normal, latent_dim)
# train normal or straight-through models
train_epochs(g_normal, d_normal, gan_normal, scaled_data, e_norm[i], n_batch[i])
summarize_performance('tuned', g_normal, latent_dim)
We can then define the configuration, models, and call train() to start the training process.
The paper recommends using a batch size of 16 for images sized between 4×4 and 128×128 before reducing the size. It also recommends training each phase for about 800K images. The paper also recommends a latent space of 512 dimensions.
The models are defined with six levels of growth to meet the 128×128 pixel size of our dataset. We also shrink the latent space accordingly to 100 dimensions.
Instead of keeping the batch size and number of epochs constant, we vary it to speed up the training process, using larger batch sizes for early training phases and smaller batch sizes for later training phases for fine-tuning and stability. Additionally, fewer training epochs are used for the smaller models and more epochs for the larger models.
The choice of batch sizes and training epochs is somewhat arbitrary and you may want to experiment with different values and review their effects.
# number of growth phases, e.g. 6 == [4, 8, 16, 32, 64, 128]
n_blocks = 6
# size of the latent space
latent_dim = 100
# define models
d_models = define_discriminator(n_blocks)
# define models
g_models = define_generator(latent_dim, n_blocks)
# define composite models
gan_models = define_composite(d_models, g_models)
# load image data
dataset = load_real_samples('img_align_celeba_128.npz')
print('Loaded', dataset.shape)
# train model
n_batch = [16, 16, 16, 8, 4, 4]
# 10 epochs == 500K images per training phase
n_epochs = [5, 8, 8, 10, 10, 10]
train(g_models, d_models, gan_models, dataset, latent_dim, n_epochs, n_epochs, n_batch)
We can tie all of this together.
The complete example of training a progressive growing generative adversarial network on the celebrity faces dataset is listed below.
# example of progressive growing gan on celebrity faces dataset
from math import sqrt
from numpy import load
from numpy import asarray
from numpy import zeros
from numpy import ones
from numpy.random import randn
from numpy.random import randint
from skimage.transform import resize
from keras.optimizers import Adam
from keras.models import Sequential
from keras.models import Model
from keras.layers import Input
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import Reshape
from keras.layers import Conv2D
from keras.layers import UpSampling2D
from keras.layers import AveragePooling2D
from keras.layers import LeakyReLU
from keras.layers import Layer
from keras.layers import Add
from keras.constraints import max_norm
from keras.initializers import RandomNormal
from keras import backend
from matplotlib import pyplot
# pixel-wise feature vector normalization layer
class PixelNormalization(Layer):
# initialize the layer
def __init__(self, **kwargs):
super(PixelNormalization, self).__init__(**kwargs)
# perform the operation
def call(self, inputs):
# calculate square pixel values
values = inputs**2.0
# calculate the mean pixel values
mean_values = backend.mean(values, axis=-1, keepdims=True)
# ensure the mean is not zero
mean_values += 1.0e-8
# calculate the sqrt of the mean squared value (L2 norm)
l2 = backend.sqrt(mean_values)
# normalize values by the l2 norm
normalized = inputs / l2
return normalized
# define the output shape of the layer
def compute_output_shape(self, input_shape):
return input_shape
# mini-batch standard deviation layer
class MinibatchStdev(Layer):
# initialize the layer
def __init__(self, **kwargs):
super(MinibatchStdev, self).__init__(**kwargs)
# perform the operation
def call(self, inputs):
# calculate the mean value for each pixel across channels
mean = backend.mean(inputs, axis=0, keepdims=True)
# calculate the squared differences between pixel values and mean
squ_diffs = backend.square(inputs - mean)
# calculate the average of the squared differences (variance)
mean_sq_diff = backend.mean(squ_diffs, axis=0, keepdims=True)
# add a small value to avoid a blow-up when we calculate stdev
mean_sq_diff += 1e-8
# square root of the variance (stdev)
stdev = backend.sqrt(mean_sq_diff)
# calculate the mean standard deviation across each pixel coord
mean_pix = backend.mean(stdev, keepdims=True)
# scale this up to be the size of one input feature map for each sample
shape = backend.shape(inputs)
output = backend.tile(mean_pix, (shape[0], shape[1], shape[2], 1))
# concatenate with the output
combined = backend.concatenate([inputs, output], axis=-1)
return combined
# define the output shape of the layer
def compute_output_shape(self, input_shape):
# create a copy of the input shape as a list
input_shape = list(input_shape)
# add one to the channel dimension (assume channels-last)
input_shape[-1] += 1
# convert list to a tuple
return tuple(input_shape)
# weighted sum output
class WeightedSum(Add):
# init with default value
def __init__(self, alpha=0.0, **kwargs):
super(WeightedSum, self).__init__(**kwargs)
self.alpha = backend.variable(alpha, name='ws_alpha')
# output a weighted sum of inputs
def _merge_function(self, inputs):
# only supports a weighted sum of two inputs
assert (len(inputs) == 2)
# ((1-a) * input1) + (a * input2)
output = ((1.0 - self.alpha) * inputs[0]) + (self.alpha * inputs[1])
return output
# calculate wasserstein loss
def wasserstein_loss(y_true, y_pred):
return backend.mean(y_true * y_pred)
# add a discriminator block
def add_discriminator_block(old_model, n_input_layers=3):
# weight initialization
init = RandomNormal(stddev=0.02)
# weight constraint
const = max_norm(1.0)
# get shape of existing model
in_shape = list(old_model.input.shape)
# define new input shape as double the size
input_shape = (in_shape[-2].value*2, in_shape[-2].value*2, in_shape[-1].value)
in_image = Input(shape=input_shape)
# define new input processing layer
d = Conv2D(128, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(in_image)
d = LeakyReLU(alpha=0.2)(d)
# define new block
d = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(d)
d = LeakyReLU(alpha=0.2)(d)
d = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(d)
d = LeakyReLU(alpha=0.2)(d)
d = AveragePooling2D()(d)
block_new = d
# skip the input, 1x1 and activation for the old model
for i in range(n_input_layers, len(old_model.layers)):
d = old_model.layers[i](d)
# define straight-through model
model1 = Model(in_image, d)
# compile model
model1.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8))
# downsample the new larger image
downsample = AveragePooling2D()(in_image)
# connect old input processing to downsampled new input
block_old = old_model.layers[1](downsample)
block_old = old_model.layers[2](block_old)
# fade in output of old model input layer with new input
d = WeightedSum()([block_old, block_new])
# skip the input, 1x1 and activation for the old model
for i in range(n_input_layers, len(old_model.layers)):
d = old_model.layers[i](d)
# define straight-through model
model2 = Model(in_image, d)
# compile model
model2.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8))
return [model1, model2]
# define the discriminator models for each image resolution
def define_discriminator(n_blocks, input_shape=(4,4,3)):
# weight initialization
init = RandomNormal(stddev=0.02)
# weight constraint
const = max_norm(1.0)
model_list = list()
# base model input
in_image = Input(shape=input_shape)
# conv 1x1
d = Conv2D(128, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(in_image)
d = LeakyReLU(alpha=0.2)(d)
# conv 3x3 (output block)
d = MinibatchStdev()(d)
d = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(d)
d = LeakyReLU(alpha=0.2)(d)
# conv 4x4
d = Conv2D(128, (4,4), padding='same', kernel_initializer=init, kernel_constraint=const)(d)
d = LeakyReLU(alpha=0.2)(d)
# dense output layer
d = Flatten()(d)
out_class = Dense(1)(d)
# define model
model = Model(in_image, out_class)
# compile model
model.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8))
# store model
model_list.append([model, model])
# create submodels
for i in range(1, n_blocks):
# get prior model without the fade-on
old_model = model_list[i - 1][0]
# create new model for next resolution
models = add_discriminator_block(old_model)
# store model
model_list.append(models)
return model_list
# add a generator block
def add_generator_block(old_model):
# weight initialization
init = RandomNormal(stddev=0.02)
# weight constraint
const = max_norm(1.0)
# get the end of the last block
block_end = old_model.layers[-2].output
# upsample, and define new block
upsampling = UpSampling2D()(block_end)
g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(upsampling)
g = PixelNormalization()(g)
g = LeakyReLU(alpha=0.2)(g)
g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(g)
g = PixelNormalization()(g)
g = LeakyReLU(alpha=0.2)(g)
# add new output layer
out_image = Conv2D(3, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(g)
# define model
model1 = Model(old_model.input, out_image)
# get the output layer from old model
out_old = old_model.layers[-1]
# connect the upsampling to the old output layer
out_image2 = out_old(upsampling)
# define new output image as the weighted sum of the old and new models
merged = WeightedSum()([out_image2, out_image])
# define model
model2 = Model(old_model.input, merged)
return [model1, model2]
# define generator models
def define_generator(latent_dim, n_blocks, in_dim=4):
# weight initialization
init = RandomNormal(stddev=0.02)
# weight constraint
const = max_norm(1.0)
model_list = list()
# base model latent input
in_latent = Input(shape=(latent_dim,))
# linear scale up to activation maps
g = Dense(128 * in_dim * in_dim, kernel_initializer=init, kernel_constraint=const)(in_latent)
g = Reshape((in_dim, in_dim, 128))(g)
# conv 4x4, input block
g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(g)
g = PixelNormalization()(g)
g = LeakyReLU(alpha=0.2)(g)
# conv 3x3
g = Conv2D(128, (3,3), padding='same', kernel_initializer=init, kernel_constraint=const)(g)
g = PixelNormalization()(g)
g = LeakyReLU(alpha=0.2)(g)
# conv 1x1, output block
out_image = Conv2D(3, (1,1), padding='same', kernel_initializer=init, kernel_constraint=const)(g)
# define model
model = Model(in_latent, out_image)
# store model
model_list.append([model, model])
# create submodels
for i in range(1, n_blocks):
# get prior model without the fade-on
old_model = model_list[i - 1][0]
# create new model for next resolution
models = add_generator_block(old_model)
# store model
model_list.append(models)
return model_list
# define composite models for training generators via discriminators
def define_composite(discriminators, generators):
model_list = list()
# create composite models
for i in range(len(discriminators)):
g_models, d_models = generators[i], discriminators[i]
# straight-through model
d_models[0].trainable = False
model1 = Sequential()
model1.add(g_models[0])
model1.add(d_models[0])
model1.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8))
# fade-in model
d_models[1].trainable = False
model2 = Sequential()
model2.add(g_models[1])
model2.add(d_models[1])
model2.compile(loss=wasserstein_loss, optimizer=Adam(lr=0.001, beta_1=0, beta_2=0.99, epsilon=10e-8))
# store
model_list.append([model1, model2])
return model_list
# load dataset
def load_real_samples(filename):
# load dataset
data = load(filename)
# extract numpy array
X = data['arr_0']
# convert from ints to floats
X = X.astype('float32')
# scale from [0,255] to [-1,1]
X = (X - 127.5) / 127.5
return X
# select real samples
def generate_real_samples(dataset, n_samples):
# choose random instances
ix = randint(0, dataset.shape[0], n_samples)
# select images
X = dataset[ix]
# generate class labels
y = ones((n_samples, 1))
return X, y
# generate points in latent space as input for the generator
def generate_latent_points(latent_dim, n_samples):
# generate points in the latent space
x_input = randn(latent_dim * n_samples)
# reshape into a batch of inputs for the network
x_input = x_input.reshape(n_samples, latent_dim)
return x_input
# use the generator to generate n fake examples, with class labels
def generate_fake_samples(generator, latent_dim, n_samples):
# generate points in latent space
x_input = generate_latent_points(latent_dim, n_samples)
# predict outputs
X = generator.predict(x_input)
# create class labels
y = -ones((n_samples, 1))
return X, y
# update the alpha value on each instance of WeightedSum
def update_fadein(models, step, n_steps):
# calculate current alpha (linear from 0 to 1)
alpha = step / float(n_steps - 1)
# update the alpha for each model
for model in models:
for layer in model.layers:
if isinstance(layer, WeightedSum):
backend.set_value(layer.alpha, alpha)
# train a generator and discriminator
def train_epochs(g_model, d_model, gan_model, dataset, n_epochs, n_batch, fadein=False):
# calculate the number of batches per training epoch
bat_per_epo = int(dataset.shape[0] / n_batch)
# calculate the number of training iterations
n_steps = bat_per_epo * n_epochs
# calculate the size of half a batch of samples
half_batch = int(n_batch / 2)
# manually enumerate epochs
for i in range(n_steps):
# update alpha for all WeightedSum layers when fading in new blocks
if fadein:
update_fadein([g_model, d_model, gan_model], i, n_steps)
# prepare real and fake samples
X_real, y_real = generate_real_samples(dataset, half_batch)
X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch)
# update discriminator model
d_loss1 = d_model.train_on_batch(X_real, y_real)
d_loss2 = d_model.train_on_batch(X_fake, y_fake)
# update the generator via the discriminator's error
z_input = generate_latent_points(latent_dim, n_batch)
y_real2 = ones((n_batch, 1))
g_loss = gan_model.train_on_batch(z_input, y_real2)
# summarize loss on this batch
print('>%d, d1=%.3f, d2=%.3f g=%.3f' % (i+1, d_loss1, d_loss2, g_loss))
# scale images to preferred size
def scale_dataset(images, new_shape):
images_list = list()
for image in images:
# resize with nearest neighbor interpolation
new_image = resize(image, new_shape, 0)
# store
images_list.append(new_image)
return asarray(images_list)
# generate samples and save as a plot and save the model
def summarize_performance(status, g_model, latent_dim, n_samples=25):
# devise name
gen_shape = g_model.output_shape
name = '%03dx%03d-%s' % (gen_shape[1], gen_shape[2], status)
# generate images
X, _ = generate_fake_samples(g_model, latent_dim, n_samples)
# normalize pixel values to the range [0,1]
X = (X - X.min()) / (X.max() - X.min())
# plot real images
square = int(sqrt(n_samples))
for i in range(n_samples):
pyplot.subplot(square, square, 1 + i)
pyplot.axis('off')
pyplot.imshow(X[i])
# save plot to file
filename1 = 'plot_%s.png' % (name)
pyplot.savefig(filename1)
pyplot.close()
# save the generator model
filename2 = 'model_%s.h5' % (name)
g_model.save(filename2)
print('>Saved: %s and %s' % (filename1, filename2))
# train the generator and discriminator
def train(g_models, d_models, gan_models, dataset, latent_dim, e_norm, e_fadein, n_batch):
# fit the baseline model
g_normal, d_normal, gan_normal = g_models[0][0], d_models[0][0], gan_models[0][0]
# scale dataset to appropriate size
gen_shape = g_normal.output_shape
scaled_data = scale_dataset(dataset, gen_shape[1:])
print('Scaled Data', scaled_data.shape)
# train normal or straight-through models
train_epochs(g_normal, d_normal, gan_normal, scaled_data, e_norm[0], n_batch[0])
summarize_performance('tuned', g_normal, latent_dim)
# process each level of growth
for i in range(1, len(g_models)):
# retrieve models for this level of growth
[g_normal, g_fadein] = g_models[i]
[d_normal, d_fadein] = d_models[i]
[gan_normal, gan_fadein] = gan_models[i]
# scale dataset to appropriate size
gen_shape = g_normal.output_shape
scaled_data = scale_dataset(dataset, gen_shape[1:])
print('Scaled Data', scaled_data.shape)
# train fade-in models for next level of growth
train_epochs(g_fadein, d_fadein, gan_fadein, scaled_data, e_fadein[i], n_batch[i], True)
summarize_performance('faded', g_normal, latent_dim)
# train normal or straight-through models
train_epochs(g_normal, d_normal, gan_normal, scaled_data, e_norm[i], n_batch[i])
summarize_performance('tuned', g_normal, latent_dim)
# number of growth phases, e.g. 6 == [4, 8, 16, 32, 64, 128]
n_blocks = 6
# size of the latent space
latent_dim = 100
# define models
d_models = define_discriminator(n_blocks)
# define models
g_models = define_generator(latent_dim, n_blocks)
# define composite models
gan_models = define_composite(d_models, g_models)
# load image data
dataset = load_real_samples('img_align_celeba_128.npz')
print('Loaded', dataset.shape)
# train model
n_batch = [16, 16, 16, 8, 4, 4]
# 10 epochs == 500K images per training phase
n_epochs = [5, 8, 8, 10, 10, 10]
train(g_models, d_models, gan_models, dataset, latent_dim, n_epochs, n_epochs, n_batch)
Note: The example can be run on the CPU, although a GPU is recommended.
Running the example may take a number of hours to complete on modern GPU hardware.
Note: Your specific results will vary given the stochastic nature of the learning algorithm. Consider running the example a few times.
If loss values during the training iterations go to zero or very large/small numbers, this may be an example of a failure mode and may require a restart of the training process.
Running the example first reports the successful loading of the prepared dataset and the scaling of the dataset to the first image size, then reports the loss of each model for each step of the training process.
Loaded (50000, 128, 128, 3) Scaled Data (50000, 4, 4, 3) >1, d1=0.993, d2=0.001 g=0.951 >2, d1=0.861, d2=0.118 g=0.982 >3, d1=0.829, d2=0.126 g=0.875 >4, d1=0.774, d2=0.202 g=0.912 >5, d1=0.687, d2=0.035 g=0.911 ...
Plots of generated images and the generator model are saved after each fade-in training phase with filenames like:
- plot_008x008-faded.png
- model_008x008-faded.h5
Plots and models are also saved after each tuning phase, with filenames like:
- plot_008x008-tuned.png
- model_008x008-tuned.h5
Reviewing plots of the generated images at each point helps to see the progression both in the size of supported images and their quality before and after the tuning phase.
For example, below is a sample of images generated after the first 4×4 training phase (plot_004x004-tuned.png). At this point, we cannot see much at all.

Synthetic Celebrity Faces at 4×4 Resolution Generated by the Progressive Growing GAN
Reviewing generated images after the fade-in training phase for 8×8 images shows more structure (plot_008x008-faded.png). The images are blocky but we can see faces.

Synthetic Celebrity Faces at 8×8 Resolution After Fade-In Generated by the Progressive Growing GAN
Next, we can contrast the generated images for 16×16 after the fade-in training phase (plot_016x016-faded.png) and after the tuning training phase (plot_016x016-tuned.png).
We can see that the images are clearly faces and we can see that the fine-tuning phase appears to improve the coloring or tone of the faces and perhaps the structure.

Synthetic Celebrity Faces at 16×16 Resolution After Fade-In Generated by the Progressive Growing GAN

Synthetic Celebrity Faces at 16×16 Resolution After Tuning Generated by the Progressive Growing GAN
Finally, we can review generated faces after tuning for the remaining 32×32, 64×64, and 128×128 resolutions. We can see that each step in resolution, the image quality is improved, allowing the model to fill in more structure and detail.
Although not perfect, the generated images show that the progressive growing GAN is capable of not only generating plausible human faces at different resolutions, but it is able to scale building upon what was learned at lower resolutions to generate plausible faces at higher resolutions.

Synthetic Celebrity Faces at 32×32 Resolution After Tuning Generated by the Progressive Growing GAN

Synthetic Celebrity Faces at 64×64 Resolution After Tuning Generated by the Progressive Growing GAN

Synthetic Celebrity Faces at 128×128 Resolution After Tuning Generated by the Progressive Growing GAN
Now that we have seen how the generator models can be fit, next we can see how we might load and use a saved generator model.
How to Synthesize Images With a Progressive Growing GAN Model
In this section, we will explore how to load a generator model and use it to generate synthetic images on demand.
The saved Keras models can be loaded via the load_model() function.
Because the generator models use custom layers, we must specify how to load the custom layers. This is achieved by providing a dict to the load_model() function that maps each of the custom layer names to the appropriate class.
...
# load model
cust = {'PixelNormalization': PixelNormalization, 'MinibatchStdev': MinibatchStdev, 'WeightedSum': WeightedSum}
model = load_model('model_016x016-tuned.h5', cust)
We can then use the generate_latent_points() function from the previous section to generate points in latent space as input for the generator model.
... # size of the latent space latent_dim = 100 # number of images to generate n_images = 25 # generate images latent_points = generate_latent_points(latent_dim, n_images) # generate images X = model.predict(latent_points)
We can then plot the results by first scaling the pixel values to the range [0,1] and plotting each image, in this case in a square grid pattern.
# create a plot of generated images
def plot_generated(images, n_images):
# plot images
square = int(sqrt(n_images))
# normalize pixel values to the range [0,1]
images = (images - images.min()) / (images.max() - images.min())
for i in range(n_images):
# define subplot
pyplot.subplot(square, square, 1 + i)
# turn off axis
pyplot.axis('off')
# plot raw pixel data
pyplot.imshow(images[i])
pyplot.show()
Tying this together, the complete example of loading a saved progressive growing GAN generator model and using it to generate new faces is listed below.
In this case, we demonstrate loading the tuned model for generating 16×16 faces.
# example of loading the generator model and generating images
from math import sqrt
from numpy import asarray
from numpy.random import randn
from numpy.random import randint
from keras.layers import Layer
from keras.layers import Add
from keras import backend
from keras.models import load_model
from matplotlib import pyplot
# pixel-wise feature vector normalization layer
class PixelNormalization(Layer):
# initialize the layer
def __init__(self, **kwargs):
super(PixelNormalization, self).__init__(**kwargs)
# perform the operation
def call(self, inputs):
# calculate square pixel values
values = inputs**2.0
# calculate the mean pixel values
mean_values = backend.mean(values, axis=-1, keepdims=True)
# ensure the mean is not zero
mean_values += 1.0e-8
# calculate the sqrt of the mean squared value (L2 norm)
l2 = backend.sqrt(mean_values)
# normalize values by the l2 norm
normalized = inputs / l2
return normalized
# define the output shape of the layer
def compute_output_shape(self, input_shape):
return input_shape
# mini-batch standard deviation layer
class MinibatchStdev(Layer):
# initialize the layer
def __init__(self, **kwargs):
super(MinibatchStdev, self).__init__(**kwargs)
# perform the operation
def call(self, inputs):
# calculate the mean value for each pixel across channels
mean = backend.mean(inputs, axis=0, keepdims=True)
# calculate the squared differences between pixel values and mean
squ_diffs = backend.square(inputs - mean)
# calculate the average of the squared differences (variance)
mean_sq_diff = backend.mean(squ_diffs, axis=0, keepdims=True)
# add a small value to avoid a blow-up when we calculate stdev
mean_sq_diff += 1e-8
# square root of the variance (stdev)
stdev = backend.sqrt(mean_sq_diff)
# calculate the mean standard deviation across each pixel coord
mean_pix = backend.mean(stdev, keepdims=True)
# scale this up to be the size of one input feature map for each sample
shape = backend.shape(inputs)
output = backend.tile(mean_pix, (shape[0], shape[1], shape[2], 1))
# concatenate with the output
combined = backend.concatenate([inputs, output], axis=-1)
return combined
# define the output shape of the layer
def compute_output_shape(self, input_shape):
# create a copy of the input shape as a list
input_shape = list(input_shape)
# add one to the channel dimension (assume channels-last)
input_shape[-1] += 1
# convert list to a tuple
return tuple(input_shape)
# weighted sum output
class WeightedSum(Add):
# init with default value
def __init__(self, alpha=0.0, **kwargs):
super(WeightedSum, self).__init__(**kwargs)
self.alpha = backend.variable(alpha, name='ws_alpha')
# output a weighted sum of inputs
def _merge_function(self, inputs):
# only supports a weighted sum of two inputs
assert (len(inputs) == 2)
# ((1-a) * input1) + (a * input2)
output = ((1.0 - self.alpha) * inputs[0]) + (self.alpha * inputs[1])
return output
# generate points in latent space as input for the generator
def generate_latent_points(latent_dim, n_samples):
# generate points in the latent space
x_input = randn(latent_dim * n_samples)
# reshape into a batch of inputs for the network
z_input = x_input.reshape(n_samples, latent_dim)
return z_input
# create a plot of generated images
def plot_generated(images, n_images):
# plot images
square = int(sqrt(n_images))
# normalize pixel values to the range [0,1]
images = (images - images.min()) / (images.max() - images.min())
for i in range(n_images):
# define subplot
pyplot.subplot(square, square, 1 + i)
# turn off axis
pyplot.axis('off')
# plot raw pixel data
pyplot.imshow(images[i])
pyplot.show()
# load model
cust = {'PixelNormalization': PixelNormalization, 'MinibatchStdev': MinibatchStdev, 'WeightedSum': WeightedSum}
model = load_model('model_016x016-tuned.h5', cust)
# size of the latent space
latent_dim = 100
# number of images to generate
n_images = 25
# generate images
latent_points = generate_latent_points(latent_dim, n_images)
# generate images
X = model.predict(latent_points)
# plot the result
plot_generated(X, n_images)
Running the example loads the model and generates 25 faces that are plotted in a 5×5 grid.

Plot of 25 Synthetic Faces with 16×16 Resolution Generated With a Final Progressive Growing GAN Model
We can then change the filename to a different model, such as the tuned model for generating 128×128 faces.
...
model = load_model('model_128x128-tuned.h5', cust)
Re-running the example generates a plot of higher-resolution synthetic faces.

Plot of 25 Synthetic Faces With 128×128 Resolution Generated With a Final Progressive Growing GAN Model
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Change Alpha via Callback. Update the example to use a Keras callback to update the alpha value for the WeightedSum layers during fade-in training.
- Pre-Scale Dataset. Update the example to pre-scale each dataset and save each version to file to be loaded when needed during training.
- Equalized Learning Rate. Update the example to implement the equalized learning rate weight scaling method described in the paper.
- Progression in Number of Filters. Update the example to decrease the number of filters with depth in the generator and increase the number of filters with depth in the discriminator to match the configuration in the paper.
- Larger Image Size. Update the example to generate large image sizes, such as 512×512.
If you explore any of these extensions, I’d love to know.
Post your findings in the comments below.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Official
- Progressive Growing of GANs for Improved Quality, Stability, and Variation, 2017.
- Progressive Growing of GANs for Improved Quality, Stability, and Variation, Official.
- progressive_growing_of_gans Project (official), GitHub.
- Progressive Growing of GANs for Improved Quality, Stability, and Variation. Open Review.
- Progressive Growing of GANs for Improved Quality, Stability, and Variation, YouTube.
- Progressive growing of GANs for improved quality, stability and variation, KeyNote, YouTube.
API
- Keras Datasets API.
- Keras Sequential Model API
- Keras Convolutional Layers API
- How can I “freeze” Keras layers?
- Keras Contrib Project
- skimage.transform.resize API
Articles
- Keras-progressive_growing_of_gans Project, GitHub.
- Hands-On-Generative-Adversarial-Networks-with-Keras Project, GitHub.
Summary
In this tutorial, you discovered how to implement and train a progressive growing generative adversarial network for generating celebrity faces.
Specifically, you learned:
- How to prepare the celebrity faces dataset for training a progressive growing GAN model.
- How to define and train the progressive growing GAN on the celebrity faces dataset.
- How to load saved generator models and use them for generating ad hoc synthetic celebrity faces.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post How to Train a Progressive Growing GAN in Keras for Synthesizing Faces appeared first on Machine Learning Mastery.
