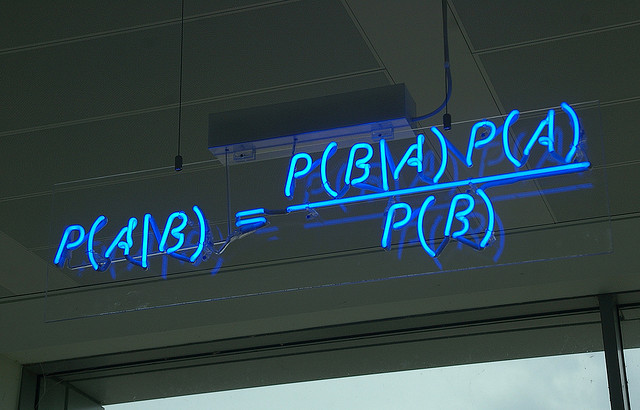Author: Jason Brownlee
In this tutorial you are going to learn about the Naive Bayes algorithm including how it works and how to implement it from scratch in Python (without libraries).
We can use probability to make predictions in machine learning. Perhaps the most widely used example is called the Naive Bayes algorithm. Not only is it straightforward to understand, but it also achieves surprisingly good results on a wide range of problems.
After completing this tutorial you will know:
- How to calculate the probabilities required by the Naive Bayes algorithm.
- How to implement the Naive Bayes algorithm from scratch.
- How to apply Naive Bayes to a real-world predictive modeling problem.
Discover how to code ML algorithms from scratch including kNN, decision trees, neural nets, ensembles and much more in my new book, with full Python code and no fancy libraries.
Let’s get started.
- Update Dec/2014: Original implementation.
- Update Oct/2019: Rewrote the tutorial and code from the ground-up.
Code a Naive Bayes Classifier From Scratch in Python (with no libraries)
Photo by Matt Buck, some rights reserved
Overview
This section provides a brief overview of the Naive Bayes algorithm and the Iris flowers dataset that we will use in this tutorial.
Naive Bayes
Bayes’ Theorem provides a way that we can calculate the probability of a piece of data belonging to a given class, given our prior knowledge. Bayes’ Theorem is stated as:
- P(class|data) = (P(data|class) * P(class)) / P(data)
Where P(class|data) is the probability of class given the provided data.
For an in-depth introduction to Bayes Theorem, see the tutorial:
Naive Bayes is a classification algorithm for binary (two-class) and multiclass classification problems. It is called Naive Bayes or idiot Bayes because the calculations of the probabilities for each class are simplified to make their calculations tractable.
Rather than attempting to calculate the probabilities of each attribute value, they are assumed to be conditionally independent given the class value.
This is a very strong assumption that is most unlikely in real data, i.e. that the attributes do not interact. Nevertheless, the approach performs surprisingly well on data where this assumption does not hold.
For an in-depth introduction to Naive Bayes, see the tutorial:
Iris Flower Species Dataset
In this tutorial we will use the Iris Flower Species Dataset.
The Iris Flower Dataset involves predicting the flower species given measurements of iris flowers.
It is a multiclass classification problem. The number of observations for each class is balanced. There are 150 observations with 4 input variables and 1 output variable. The variable names are as follows:
- Sepal length in cm.
- Sepal width in cm.
- Petal length in cm.
- Petal width in cm.
- Class
A sample of the first 5 rows is listed below.
5.1,3.5,1.4,0.2,Iris-setosa 4.9,3.0,1.4,0.2,Iris-setosa 4.7,3.2,1.3,0.2,Iris-setosa 4.6,3.1,1.5,0.2,Iris-setosa 5.0,3.6,1.4,0.2,Iris-setosa ...
The baseline performance on the problem is approximately 33%.
Download the dataset and save it into your current working directory with the filename iris.csv.
Naive Bayes Tutorial (in 5 easy steps)
First we will develop each piece of the algorithm in this section, then we will tie all of the elements together into a working implementation applied to a real dataset in the next section.
This Naive Bayes tutorial is broken down into 5 parts:
- Step 1: Separate By Class.
- Step 2: Summarize Dataset.
- Step 3: Summarize Data By Class.
- Step 4: Gaussian Probability Density Function.
- Step 5: Class Probabilities.
These steps will provide the foundation that you need to implement Naive Bayes from scratch and apply it to your own predictive modeling problems.
Note: This tutorial assumes that you are using Python 3. If you need help installing Python, see this tutorial:
Note: if you are using Python 2.7, you must change all calls to the items() function on dictionary objects to iteritems().
Step 1: Separate By Class
We will need to calculate the probability of data by the class they belong to, the so-called base rate.
This means that we will first need to separate our training data by class. A relatively straightforward operation.
We can create a dictionary object where each key is the class value and then add a list of all the records as the value in the dictionary.
Below is a function named separate_by_class() that implements this approach. It assumes that the last column in each row is the class value.
# Split the dataset by class values, returns a dictionary def separate_by_class(dataset): separated = dict() for i in range(len(dataset)): vector = dataset[i] class_value = vector[-1] if (class_value not in separated): separated[class_value] = list() separated[class_value].append(vector) return separated
We can contrive a small dataset to test out this function.
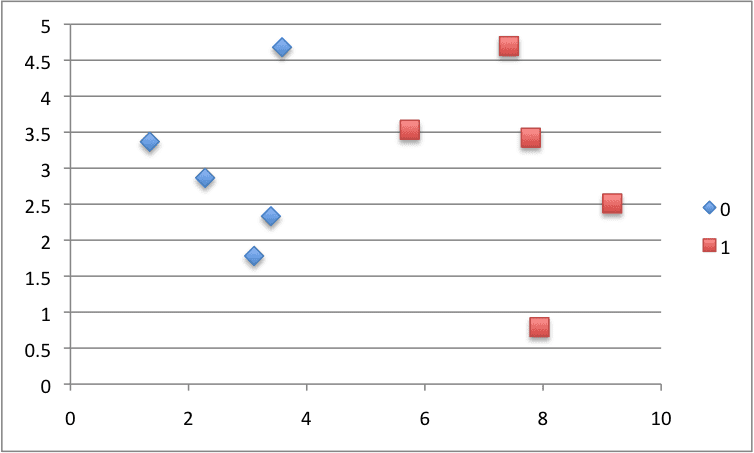
X1 X2 Y 3.393533211 2.331273381 0 3.110073483 1.781539638 0 1.343808831 3.368360954 0 3.582294042 4.67917911 0 2.280362439 2.866990263 0 7.423436942 4.696522875 1 5.745051997 3.533989803 1 9.172168622 2.511101045 1 7.792783481 3.424088941 1 7.939820817 0.791637231 1
We can plot this dataset and use separate colors for each class.
Scatter Plot of Small Contrived Dataset for Testing the Naive Bayes Algorithm
Putting this all together, we can test our separate_by_class() function on the contrived dataset.
# Example of separating data by class value # Split the dataset by class values, returns a dictionary def separate_by_class(dataset): separated = dict() for i in range(len(dataset)): vector = dataset[i] class_value = vector[-1] if (class_value not in separated): separated[class_value] = list() separated[class_value].append(vector) return separated # Test separating data by class dataset = [[3.393533211,2.331273381,0], [3.110073483,1.781539638,0], [1.343808831,3.368360954,0], [3.582294042,4.67917911,0], [2.280362439,2.866990263,0], [7.423436942,4.696522875,1], [5.745051997,3.533989803,1], [9.172168622,2.511101045,1], [7.792783481,3.424088941,1], [7.939820817,0.791637231,1]] separated = separate_by_class(dataset) for label in separated: print(label) for row in separated[label]: print(row)
Running the example sorts observations in the dataset by their class value, then prints the class value followed by all identified records.
0 [3.393533211, 2.331273381, 0] [3.110073483, 1.781539638, 0] [1.343808831, 3.368360954, 0] [3.582294042, 4.67917911, 0] [2.280362439, 2.866990263, 0] 1 [7.423436942, 4.696522875, 1] [5.745051997, 3.533989803, 1] [9.172168622, 2.511101045, 1] [7.792783481, 3.424088941, 1] [7.939820817, 0.791637231, 1]
Next we can start to develop the functions needed to collect statistics.
Step 2: Summarize Dataset
We need two statistics from a given set of data.
We’ll see how these statistics are used in the calculation of probabilities in a few steps. The two statistics we require from a given dataset are the mean and the standard deviation (average deviation from the mean).
The mean is the average value and can be calculated as:
- mean = sum(x)/n * count(x)
Where x is the list of values or a column we are looking.
Below is a small function named mean() that calculates the mean of a list of numbers.
# Calculate the mean of a list of numbers def mean(numbers): return sum(numbers)/float(len(numbers))
The sample standard deviation is calculated as the mean difference from the mean value. This can be calculated as:
- standard deviation = sqrt((sum i to N (x_i – mean(x))^2) / N-1)
You can see that we square the difference between the mean and a given value, calculate the average squared difference from the mean, then take the square root to return the units back to their original value.
Below is a small function named standard_deviation() that calculates the standard deviation of a list of numbers. You will notice that it calculates the mean. It might be more efficient to calculate the mean of a list of numbers once and pass it to the standard_deviation() function as a parameter. You can explore this optimization if you’re interested later.
from math import sqrt # Calculate the standard deviation of a list of numbers def stdev(numbers): avg = mean(numbers) variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1) return sqrt(variance)
We require the mean and standard deviation statistics to be calculated for each input attribute or each column of our data.
We can do that by gathering all of the values for each column into a list and calculating the mean and standard deviation on that list. Once calculated, we can gather the statistics together into a list or tuple of statistics. Then, repeat this operation for each column in the dataset and return a list of tuples of statistics.
Below is a function named summarize_dataset() that implements this approach. It uses some Python tricks to cut down on the number of lines required.
# Calculate the mean, stdev and count for each column in a dataset def summarize_dataset(dataset): summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)] del(summaries[-1]) return summaries
The first trick is the use of the zip() function that will aggregate elements from each provided argument. We pass in the dataset to the zip() function with the * operator that separates the dataset (that is a list of lists) into separate lists for each row. The zip() function then iterates over each element of each row and returns a column from the dataset as a list of numbers. A clever little trick.
We then calculate the mean, standard deviation and count of rows in each column. A tuple is created from these 3 numbers and a list of these tuples is stored. We then remove the statistics for the class variable as we will not need these statistics.
Let’s test all of these functions on our contrived dataset from above. Below is the complete example.
# Example of summarizing a dataset from math import sqrt # Calculate the mean of a list of numbers def mean(numbers): return sum(numbers)/float(len(numbers)) # Calculate the standard deviation of a list of numbers def stdev(numbers): avg = mean(numbers) variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1) return sqrt(variance) # Calculate the mean, stdev and count for each column in a dataset def summarize_dataset(dataset): summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)] del(summaries[-1]) return summaries # Test summarizing a dataset dataset = [[3.393533211,2.331273381,0], [3.110073483,1.781539638,0], [1.343808831,3.368360954,0], [3.582294042,4.67917911,0], [2.280362439,2.866990263,0], [7.423436942,4.696522875,1], [5.745051997,3.533989803,1], [9.172168622,2.511101045,1], [7.792783481,3.424088941,1], [7.939820817,0.791637231,1]] summary = summarize_dataset(dataset) print(summary)
Running the example prints out the list of tuples of statistics on each of the two input variables.
Interpreting the results, we can see that the mean value of X1 is 5.178333386499999 and the standard deviation of X1 is 2.7665845055177263.
[(5.178333386499999, 2.7665845055177263, 10), (2.9984683241, 1.218556343617447, 10)]
Now we are ready to use these functions on each group of rows in our dataset.
Step 3: Summarize Data By Class
We require statistics from our training dataset organized by class.
Above, we have developed the separate_by_class() function to separate a dataset into rows by class. And we have developed summarize_dataset() function to calculate summary statistics for each column.
We can put all of this together and summarize the columns in the dataset organized by class values.
Below is a function named summarize_by_class() that implements this operation. The dataset is first split by class, then statistics are calculated on each subset. The results in the form of a list of tuples of statistics are then stored in a dictionary by their class value.
# Split dataset by class then calculate statistics for each row def summarize_by_class(dataset): separated = separate_by_class(dataset) summaries = dict() for class_value, rows in separated.items(): summaries[class_value] = summarize_dataset(rows) return summaries
Again, let’s test out all of these behaviors on our contrived dataset.
# Example of summarizing data by class value from math import sqrt # Split the dataset by class values, returns a dictionary def separate_by_class(dataset): separated = dict() for i in range(len(dataset)): vector = dataset[i] class_value = vector[-1] if (class_value not in separated): separated[class_value] = list() separated[class_value].append(vector) return separated # Calculate the mean of a list of numbers def mean(numbers): return sum(numbers)/float(len(numbers)) # Calculate the standard deviation of a list of numbers def stdev(numbers): avg = mean(numbers) variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1) return sqrt(variance) # Calculate the mean, stdev and count for each column in a dataset def summarize_dataset(dataset): summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)] del(summaries[-1]) return summaries # Split dataset by class then calculate statistics for each row def summarize_by_class(dataset): separated = separate_by_class(dataset) summaries = dict() for class_value, rows in separated.items(): summaries[class_value] = summarize_dataset(rows) return summaries # Test summarizing by class dataset = [[3.393533211,2.331273381,0], [3.110073483,1.781539638,0], [1.343808831,3.368360954,0], [3.582294042,4.67917911,0], [2.280362439,2.866990263,0], [7.423436942,4.696522875,1], [5.745051997,3.533989803,1], [9.172168622,2.511101045,1], [7.792783481,3.424088941,1], [7.939820817,0.791637231,1]] summary = summarize_by_class(dataset) for label in summary: print(label) for row in summary[label]: print(row)
Running this example calculates the statistics for each input variable and prints them organized by class value. Interpreting the results, we can see that the X1 values for rows for class 0 have a mean value of 2.7420144012.
0 (2.7420144012, 0.9265683289298018, 5) (3.0054686692, 1.1073295894898725, 5) 1 (7.6146523718, 1.2344321550313704, 5) (2.9914679790000003, 1.4541931384601618, 5)
There is one more piece we need before we start calculating probabilities.
Step 4: Gaussian Probability Density Function
Calculating the probability or likelihood of observing a given real-value like X1 is difficult.
One way we can do this is to assume that X1 values are drawn from a distribution, such as a bell curve or Gaussian distribution.
A Gaussian distribution can be summarized using only two numbers: the mean and the standard deviation. Therefore, with a little math, we can estimate the probability of a given value. This piece of math is called a Gaussian Probability Distribution Function (or Gaussian PDF) and can be calculated as:
- f(x) = (1 / sqrt(2 * PI) * sigma) * exp(-((x-mean)^2 / (2 * sigma^2)))
Where sigma is the standard deviation for x, mean is the mean for x and PI is the value of pi.
Below is a function that implements this. I tried to split it up to make it more readable.
# Calculate the Gaussian probability distribution function for x def calculate_probability(x, mean, stdev): exponent = exp(-((x-mean)**2 / (2 * stdev**2 ))) return (1 / (sqrt(2 * pi) * stdev)) * exponent
Let’s test it out to see how it works. Below are some worked examples.
# Example of Gaussian PDF from math import sqrt from math import pi from math import exp # Calculate the Gaussian probability distribution function for x def calculate_probability(x, mean, stdev): exponent = exp(-((x-mean)**2 / (2 * stdev**2 ))) return (1 / (sqrt(2 * pi) * stdev)) * exponent # Test Gaussian PDF print(calculate_probability(1.0, 1.0, 1.0)) print(calculate_probability(2.0, 1.0, 1.0)) print(calculate_probability(0.0, 1.0, 1.0))
Running it prints the probability of some input values. You can see that when the value is 1 and the mean and standard deviation is 1 our input is the most likely (top of the bell curve) and has the probability of 0.39.
We can see that when we keep the statistics the same and change the x value to 1 standard deviation either side of the mean value (2 and 0 or the same distance either side of the bell curve) the probabilities of those input values are the same at 0.24.
0.3989422804014327 0.24197072451914337 0.24197072451914337
Now that we have all the pieces in place, let’s see how we can calculate the probabilities we need for the Naive Bayes classifier.
Step 5: Class Probabilities
Now it is time to use the statistics calculated from our training data to calculate probabilities for new data.
Probabilities are calculated separately for each class. This means that we first calculate the probability that a new piece of data belongs to the first class, then calculate probabilities that it belongs to the second class, and so on for all the classes.
The probability that a piece of data belongs to a class is calculated as follows:
- P(class|data) = P(X|class) * P(class)
You may note that this is different from the Bayes Theorem described above.
The division has been removed to simplify the calculation.
This means that the result is no longer strictly a probability of the data belonging to a class. The value is still maximized, meaning that the calculation for the class that results in the largest value is taken as the prediction. This is a common implementation simplification as we are often more interested in the class prediction rather than the probability.
The input variables are treated separately, giving the technique it’s name “naive“. For the above example where we have 2 input variables, the calculation of the probability that a row belongs to the first class 0 can be calculated as:
- P(class=0|X1,X2) = P(X1|class=0) * P(X2|class=0) * P(class=0)
Now you can see why we need to separate the data by class value. The Gaussian Probability Density function in the previous step is how we calculate the probability of a real value like X1 and the statistics we prepared are used in this calculation.
Below is a function named calculate_class_probabilities() that ties all of this together.
It takes a set of prepared summaries and a new row as input arguments.
First the total number of training records is calculated from the counts stored in the summary statistics. This is used in the calculation of the probability of a given class or P(class) as the ratio of rows with a given class of all rows in the training data.
Next, probabilities are calculated for each input value in the row using the Gaussian probability density function and the statistics for that column and of that class. Probabilities are multiplied together as they accumulated.
This process is repeated for each class in the dataset.
Finally a dictionary of probabilities is returned with one entry for each class.
# Calculate the probabilities of predicting each class for a given row def calculate_class_probabilities(summaries, row): total_rows = sum([summaries[label][0][2] for label in summaries]) probabilities = dict() for class_value, class_summaries in summaries.items(): probabilities[class_value] = summaries[class_value][0][2]/float(total_rows) for i in range(len(class_summaries)): mean, stdev, count = class_summaries[i] probabilities[class_value] *= calculate_probability(row[i], mean, stdev) return probabilities
Let’s tie this together with an example on the contrived dataset.
The example below first calculates the summary statistics by class for the training dataset, then uses these statistics to calculate the probability of the first record belonging to each class.
# Example of calculating class probabilities from math import sqrt from math import pi from math import exp # Split the dataset by class values, returns a dictionary def separate_by_class(dataset): separated = dict() for i in range(len(dataset)): vector = dataset[i] class_value = vector[-1] if (class_value not in separated): separated[class_value] = list() separated[class_value].append(vector) return separated # Calculate the mean of a list of numbers def mean(numbers): return sum(numbers)/float(len(numbers)) # Calculate the standard deviation of a list of numbers def stdev(numbers): avg = mean(numbers) variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1) return sqrt(variance) # Calculate the mean, stdev and count for each column in a dataset def summarize_dataset(dataset): summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)] del(summaries[-1]) return summaries # Split dataset by class then calculate statistics for each row def summarize_by_class(dataset): separated = separate_by_class(dataset) summaries = dict() for class_value, rows in separated.items(): summaries[class_value] = summarize_dataset(rows) return summaries # Calculate the Gaussian probability distribution function for x def calculate_probability(x, mean, stdev): exponent = exp(-((x-mean)**2 / (2 * stdev**2 ))) return (1 / (sqrt(2 * pi) * stdev)) * exponent # Calculate the probabilities of predicting each class for a given row def calculate_class_probabilities(summaries, row): total_rows = sum([summaries[label][0][2] for label in summaries]) probabilities = dict() for class_value, class_summaries in summaries.items(): probabilities[class_value] = summaries[class_value][0][2]/float(total_rows) for i in range(len(class_summaries)): mean, stdev, _ = class_summaries[i] probabilities[class_value] *= calculate_probability(row[i], mean, stdev) return probabilities # Test calculating class probabilities dataset = [[3.393533211,2.331273381,0], [3.110073483,1.781539638,0], [1.343808831,3.368360954,0], [3.582294042,4.67917911,0], [2.280362439,2.866990263,0], [7.423436942,4.696522875,1], [5.745051997,3.533989803,1], [9.172168622,2.511101045,1], [7.792783481,3.424088941,1], [7.939820817,0.791637231,1]] summaries = summarize_by_class(dataset) probabilities = calculate_class_probabilities(summaries, dataset[0]) print(probabilities)
Running the example prints the probabilities calculated for each class.
We can see that the probability of the first row belonging to the 0 class (0.0503) is higher than the probability of it belonging to the 1 class (0.0001). We would therefore correctly conclude that it belongs to the 0 class.
{0: 0.05032427673372075, 1: 0.00011557718379945765}
Now that we have seen how to implement the Naive Bayes algorithm, let’s apply it to the Iris flowers dataset.
Iris Flower Species Case Study
This section applies the Naive Bayes algorithm to the Iris flowers dataset.
The first step is to load the dataset and convert the loaded data to numbers that we can use with the mean and standard deviation calculations. For this we will use the helper function load_csv() to load the file, str_column_to_float() to convert string numbers to floats and str_column_to_int() to convert the class column to integer values.
We will evaluate the algorithm using k-fold cross-validation with 5 folds. This means that 150/5=30 records will be in each fold. We will use the helper functions evaluate_algorithm() to evaluate the algorithm with cross-validation and accuracy_metric() to calculate the accuracy of predictions.
A new function named predict() was developed to manage the calculation of the probabilities of a new row belonging to each class and selecting the class with the largest probability value.
Another new function named naive_bayes() was developed to manage the application of the Naive Bayes algorithm, first learning the statistics from a training dataset and using them to make predictions for a test dataset.
If you would like more help with the data loading functions used below, see the tutorial:
If you would like more help with the way the model is evaluated using cross validation, see the tutorial:
The complete example is listed below.
# Naive Bayes On The Iris Dataset
from csv import reader
from random import seed
from random import randrange
from math import sqrt
from math import exp
from math import pi
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for _ in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Split the dataset by class values, returns a dictionary
def separate_by_class(dataset):
separated = dict()
for i in range(len(dataset)):
vector = dataset[i]
class_value = vector[-1]
if (class_value not in separated):
separated[class_value] = list()
separated[class_value].append(vector)
return separated
# Calculate the mean of a list of numbers
def mean(numbers):
return sum(numbers)/float(len(numbers))
# Calculate the standard deviation of a list of numbers
def stdev(numbers):
avg = mean(numbers)
variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1)
return sqrt(variance)
# Calculate the mean, stdev and count for each column in a dataset
def summarize_dataset(dataset):
summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)]
del(summaries[-1])
return summaries
# Split dataset by class then calculate statistics for each row
def summarize_by_class(dataset):
separated = separate_by_class(dataset)
summaries = dict()
for class_value, rows in separated.items():
summaries[class_value] = summarize_dataset(rows)
return summaries
# Calculate the Gaussian probability distribution function for x
def calculate_probability(x, mean, stdev):
exponent = exp(-((x-mean)**2 / (2 * stdev**2 )))
return (1 / (sqrt(2 * pi) * stdev)) * exponent
# Calculate the probabilities of predicting each class for a given row
def calculate_class_probabilities(summaries, row):
total_rows = sum([summaries[label][0][2] for label in summaries])
probabilities = dict()
for class_value, class_summaries in summaries.items():
probabilities[class_value] = summaries[class_value][0][2]/float(total_rows)
for i in range(len(class_summaries)):
mean, stdev, _ = class_summaries[i]
probabilities[class_value] *= calculate_probability(row[i], mean, stdev)
return probabilities
# Predict the class for a given row
def predict(summaries, row):
probabilities = calculate_class_probabilities(summaries, row)
best_label, best_prob = None, -1
for class_value, probability in probabilities.items():
if best_label is None or probability > best_prob:
best_prob = probability
best_label = class_value
return best_label
# Naive Bayes Algorithm
def naive_bayes(train, test):
summarize = summarize_by_class(train)
predictions = list()
for row in test:
output = predict(summarize, row)
predictions.append(output)
return(predictions)
# Test Naive Bayes on Iris Dataset
seed(1)
filename = 'iris.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# evaluate algorithm
n_folds = 5
scores = evaluate_algorithm(dataset, naive_bayes, n_folds)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))
Running the example prints the mean classification accuracy scores on each cross-validation fold as well as the mean accuracy score.
We can see that the mean accuracy of about 95% is dramatically better than the baseline accuracy of 33%.
Scores: [93.33333333333333, 96.66666666666667, 100.0, 93.33333333333333, 93.33333333333333] Mean Accuracy: 95.333%
We can fit the model on the entire dataset and then use the model to make predictions for new observations (rows of data).
For example, the model is just a set of probabilities calculated via the summarize_by_class() function.
... # fit model model = summarize_by_class(dataset)
Once calculated, we can use them in a call to the predict() function with a row representing our new observation to predict the class label.
... # predict the label label = predict(model, row)
We also might like to know the class label (string) for a prediction. We can update the str_column_to_int() function to print the mapping of string class names to integers so we can interpret the prediction by the model.
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
print('[%s] => %d' % (value, i))
for row in dataset:
row[column] = lookup[row[column]]
return lookup
Tying this together, a complete example of fitting the Naive Bayes model on the entire dataset and making a single prediction for a new observation is listed below.
# Make Predictions with Naive Bayes On The Iris Dataset
from csv import reader
from math import sqrt
from math import exp
from math import pi
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
print('[%s] => %d' % (value, i))
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Split the dataset by class values, returns a dictionary
def separate_by_class(dataset):
separated = dict()
for i in range(len(dataset)):
vector = dataset[i]
class_value = vector[-1]
if (class_value not in separated):
separated[class_value] = list()
separated[class_value].append(vector)
return separated
# Calculate the mean of a list of numbers
def mean(numbers):
return sum(numbers)/float(len(numbers))
# Calculate the standard deviation of a list of numbers
def stdev(numbers):
avg = mean(numbers)
variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1)
return sqrt(variance)
# Calculate the mean, stdev and count for each column in a dataset
def summarize_dataset(dataset):
summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)]
del(summaries[-1])
return summaries
# Split dataset by class then calculate statistics for each row
def summarize_by_class(dataset):
separated = separate_by_class(dataset)
summaries = dict()
for class_value, rows in separated.items():
summaries[class_value] = summarize_dataset(rows)
return summaries
# Calculate the Gaussian probability distribution function for x
def calculate_probability(x, mean, stdev):
exponent = exp(-((x-mean)**2 / (2 * stdev**2 )))
return (1 / (sqrt(2 * pi) * stdev)) * exponent
# Calculate the probabilities of predicting each class for a given row
def calculate_class_probabilities(summaries, row):
total_rows = sum([summaries[label][0][2] for label in summaries])
probabilities = dict()
for class_value, class_summaries in summaries.items():
probabilities[class_value] = summaries[class_value][0][2]/float(total_rows)
for i in range(len(class_summaries)):
mean, stdev, _ = class_summaries[i]
probabilities[class_value] *= calculate_probability(row[i], mean, stdev)
return probabilities
# Predict the class for a given row
def predict(summaries, row):
probabilities = calculate_class_probabilities(summaries, row)
best_label, best_prob = None, -1
for class_value, probability in probabilities.items():
if best_label is None or probability > best_prob:
best_prob = probability
best_label = class_value
return best_label
# Make a prediction with Naive Bayes on Iris Dataset
filename = 'iris.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# fit model
model = summarize_by_class(dataset)
# define a new record
row = [5.7,2.9,4.2,1.3]
# predict the label
label = predict(model, row)
print('Data=%s, Predicted: %s' % (row, label))
Running the data first summarizes the mapping of class labels to integers and then fits the model on the entire dataset.
Then a new observation is defined (in this case I took a row from the dataset), and a predicted label is calculated. In this case our observation is predicted as belonging to class 2 which we know is “Iris-setosa”.
[Iris-virginica] => 0 [Iris-versicolor] => 1 [Iris-setosa] => 2 Data=[5.7, 2.9, 4.2, 1.3], Predicted: 1
Extensions
This section lists extensions to the tutorial that you may wish to explore.
- Log Probabilities: The conditional probabilities for each class given an attribute value are small. When they are multiplied together they result in very small values, which can lead to floating point underflow (numbers too small to represent in Python). A common fix for this is to add the log of the probabilities together. Research and implement this improvement.
- Nominal Attributes: Update the implementation to support nominal attributes. This is much similar and the summary information you can collect for each attribute is the ratio of category values for each class. Dive into the references for more information.
- Different Density Function (bernoulli or multinomial): We have looked at Gaussian Naive Bayes, but you can also look at other distributions. Implement a different distribution such as multinomial, bernoulli or kernel naive bayes that make different assumptions about the distribution of attribute values and/or their relationship with the class value.
If you try any of these extensions, let me know in the comments below.
Further Reading
Tutorials
- A Gentle Introduction to Bayes Theorem for Machine Learning
- How to Develop a Naive Bayes Classifier from Scratch in Python
- Naive Bayes Tutorial for Machine Learning
- Naive Bayes for Machine Learning
- Better Naive Bayes: 12 Tips To Get The Most From The Naive Bayes Algorithm
Books
- Section 13.6 Naive Bayes, page 353, Applied Predictive Modeling, 2013.
- Section 4.2, Statistical modeling, page 88, Data Mining: Practical Machine Learning Tools and Techniques, 2nd edition, 2005.
Summary
In this tutorial you discovered how to implement the Naive Bayes algorithm from scratch in Python.
Specifically, you learned:
- How to calculate the probabilities required by the Naive interpretation of Bayes Theorem.
- How to use probabilities to make predictions on new data.
- How to apply Naive Bayes to a real-world predictive modeling problem.
Next Step
Take action!
- Follow the tutorial and implement Naive Bayes from scratch.
- Adapt the example to another dataset.
- Follow the extensions and improve upon the implementation.
Leave a comment and share your experiences.
The post Naive Bayes Classifier From Scratch in Python appeared first on Machine Learning Mastery.