Author: Jason Brownlee
Feature selection is the process of identifying and selecting a subset of input features that are most relevant to the target variable.
Feature selection is often straightforward when working with real-valued data, such as using the Pearson’s correlation coefficient, but can be challenging when working with categorical data.
The two most commonly used feature selection methods for categorical input data when the target variable is also categorical (e.g. classification predictive modeling) are the chi-squared statistic and the mutual information statistic.
In this tutorial, you will discover how to perform feature selection with categorical input data.
After completing this tutorial, you will know:
- The breast cancer predictive modeling problem with categorical inputs and binary classification target variable.
- How to evaluate the importance of categorical features using the chi-squared and mutual information statistics.
- How to perform feature selection for categorical data when fitting and evaluating a classification model.
Let’s get started.

How to Perform Feature Selection with Categorical Data
Photo by Phil Dolby, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Breast Cancer Categorical Dataset
- Categorical Feature Selection
- Modeling With Selected Features
Breast Cancer Categorical Dataset
As the basis of this tutorial, we will use the so-called “Breast cancer” dataset that has been widely studied as a machine learning dataset since the 1980s.
The dataset classifies breast cancer patient data as either a recurrence or no recurrence of cancer. There are 286 examples and nine input variables. It is a binary classification problem.
A naive model can achieve an accuracy of 70% on this dataset. A good score is about 76% +/- 3%. We will aim for this region, but note that the models in this tutorial are not optimized; they are designed to demonstrate encoding schemes.
You can download the dataset and save the file as “breast-cancer.csv” in your current working directory.
Looking at the data, we can see that all nine input variables are categorical.
Specifically, all variables are quoted strings; some are ordinal and some are not.
'40-49','premeno','15-19','0-2','yes','3','right','left_up','no','recurrence-events' '50-59','ge40','15-19','0-2','no','1','right','central','no','no-recurrence-events' '50-59','ge40','35-39','0-2','no','2','left','left_low','no','recurrence-events' '40-49','premeno','35-39','0-2','yes','3','right','left_low','yes','no-recurrence-events' '40-49','premeno','30-34','3-5','yes','2','left','right_up','no','recurrence-events' ...
We can load this dataset into memory using the Pandas library.
... # load the dataset as a pandas DataFrame data = read_csv(filename, header=None) # retrieve numpy array dataset = data.values
Once loaded, we can split the columns into input (X) and output for modeling.
... # split into input (X) and output (y) variables X = dataset[:, :-1] y = dataset[:,-1]
Finally, we can force all fields in the input data to be string, just in case Pandas tried to map some automatically to numbers (it does try).
... # format all fields as string X = X.astype(str)
We can tie all of this together into a helpful function that we can reuse later.
# load the dataset def load_dataset(filename): # load the dataset as a pandas DataFrame data = read_csv(filename, header=None) # retrieve numpy array dataset = data.values # split into input (X) and output (y) variables X = dataset[:, :-1] y = dataset[:,-1] # format all fields as string X = X.astype(str) return X, y
Once loaded, we can split the data into training and test sets so that we can fit and evaluate a learning model.
We will use the train_test_split() function form scikit-learn and use 67% of the data for training and 33% for testing.
...
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
Tying all of these elements together, the complete example of loading, splitting, and summarizing the raw categorical dataset is listed below.
# load and summarize the dataset
from pandas import read_csv
from sklearn.model_selection import train_test_split
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# summarize
print('Train', X_train.shape, y_train.shape)
print('Test', X_test.shape, y_test.shape)
Running the example reports the size of the input and output elements of the train and test sets.
We can see that we have 191 examples for training and 95 for testing.
Train (191, 9) (191, 1) Test (95, 9) (95, 1)
Now that we are familiar with the dataset, let’s look at how we can encode it for modeling.
We can use the OrdinalEncoder() from scikit-learn to encode each variable to integers. This is a flexible class and does allow the order of the categories to be specified as arguments if any such order is known.
Note: I will leave it as an exercise to you to update the example below to try specifying the order for those variables that have a natural ordering and see if it has an impact on model performance.
The best practice when encoding variables is to fit the encoding on the training dataset, then apply it to the train and test datasets.
The function below named prepare_inputs() takes the input data for the train and test sets and encodes it using an ordinal encoding.
# prepare input data def prepare_inputs(X_train, X_test): oe = OrdinalEncoder() oe.fit(X_train) X_train_enc = oe.transform(X_train) X_test_enc = oe.transform(X_test) return X_train_enc, X_test_enc
We also need to prepare the target variable.
It is a binary classification problem, so we need to map the two class labels to 0 and 1. This is a type of ordinal encoding, and scikit-learn provides the LabelEncoder class specifically designed for this purpose. We could just as easily use the OrdinalEncoder and achieve the same result, although the LabelEncoder is designed for encoding a single variable.
The prepare_targets() function integer encodes the output data for the train and test sets.
# prepare target def prepare_targets(y_train, y_test): le = LabelEncoder() le.fit(y_train) y_train_enc = le.transform(y_train) y_test_enc = le.transform(y_test) return y_train_enc, y_test_enc
We can call these functions to prepare our data.
... # prepare input data X_train_enc, X_test_enc = prepare_inputs(X_train, X_test) # prepare output data y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
Tying this all together, the complete example of loading and encoding the input and output variables for the breast cancer categorical dataset is listed below.
# example of loading and preparing the breast cancer dataset
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# prepare input data
def prepare_inputs(X_train, X_test):
oe = OrdinalEncoder()
oe.fit(X_train)
X_train_enc = oe.transform(X_train)
X_test_enc = oe.transform(X_test)
return X_train_enc, X_test_enc
# prepare target
def prepare_targets(y_train, y_test):
le = LabelEncoder()
le.fit(y_train)
y_train_enc = le.transform(y_train)
y_test_enc = le.transform(y_test)
return y_train_enc, y_test_enc
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# prepare input data
X_train_enc, X_test_enc = prepare_inputs(X_train, X_test)
# prepare output data
y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
Now that we have loaded and prepared the breast cancer dataset, we can explore feature selection.
Categorical Feature Selection
There are two popular feature selection techniques that can be used for categorical input data and a categorical (class) target variable.
They are:
- Chi-Squared Statistic.
- Mutual Information Statistic.
Let’s take a closer look at each in turn.
Chi-Squared Feature Selection
Pearson’s chi-squared statistical hypothesis test is an example of a test for independence between categorical variables.
You can learn more about this statistical test in the tutorial:
The results of this test can be used for feature selection, where those features that are independent of the target variable can be removed from the dataset.
The scikit-learn machine library provides an implementation of the chi-squared test in the chi2() function. This function can be used in a feature selection strategy, such as selecting the top k most relevant features (largest values) via the SelectKBest class.
For example, we can define the SelectKBest class to use the chi2() function and select all features, then transform the train and test sets.
... fs = SelectKBest(score_func=chi2, k='all') fs.fit(X_train, y_train) X_train_fs = fs.transform(X_train) X_test_fs = fs.transform(X_test)
We can then print the scores for each variable (largest is better), and plot the scores for each variable as a bar graph to get an idea of how many features we should select.
...
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
Tying this together with the data preparation for the breast cancer dataset in the previous section, the complete example is listed below.
# example of chi squared feature selection for categorical data
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from matplotlib import pyplot
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# prepare input data
def prepare_inputs(X_train, X_test):
oe = OrdinalEncoder()
oe.fit(X_train)
X_train_enc = oe.transform(X_train)
X_test_enc = oe.transform(X_test)
return X_train_enc, X_test_enc
# prepare target
def prepare_targets(y_train, y_test):
le = LabelEncoder()
le.fit(y_train)
y_train_enc = le.transform(y_train)
y_test_enc = le.transform(y_test)
return y_train_enc, y_test_enc
# feature selection
def select_features(X_train, y_train, X_test):
fs = SelectKBest(score_func=chi2, k='all')
fs.fit(X_train, y_train)
X_train_fs = fs.transform(X_train)
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# prepare input data
X_train_enc, X_test_enc = prepare_inputs(X_train, X_test)
# prepare output data
y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train_enc, y_train_enc, X_test_enc)
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
Running the example first prints the scores calculated for each input feature and the target variable.
Note: your specific results may differ. Try running the example a few times.
In this case, we can see the scores are small and it is hard to get an idea from the number alone as to which features are more relevant.
Perhaps features 3, 4, 5, and 8 are most relevant.
Feature 0: 0.472553 Feature 1: 0.029193 Feature 2: 2.137658 Feature 3: 29.381059 Feature 4: 8.222601 Feature 5: 8.100183 Feature 6: 1.273822 Feature 7: 0.950682 Feature 8: 3.699989
A bar chart of the feature importance scores for each input feature is created.
This clearly shows that feature 3 might be the most relevant (according to chi-squared) and that perhaps four of the nine input features are the most relevant.
We could set k=4 When configuring the SelectKBest to select these top four features.
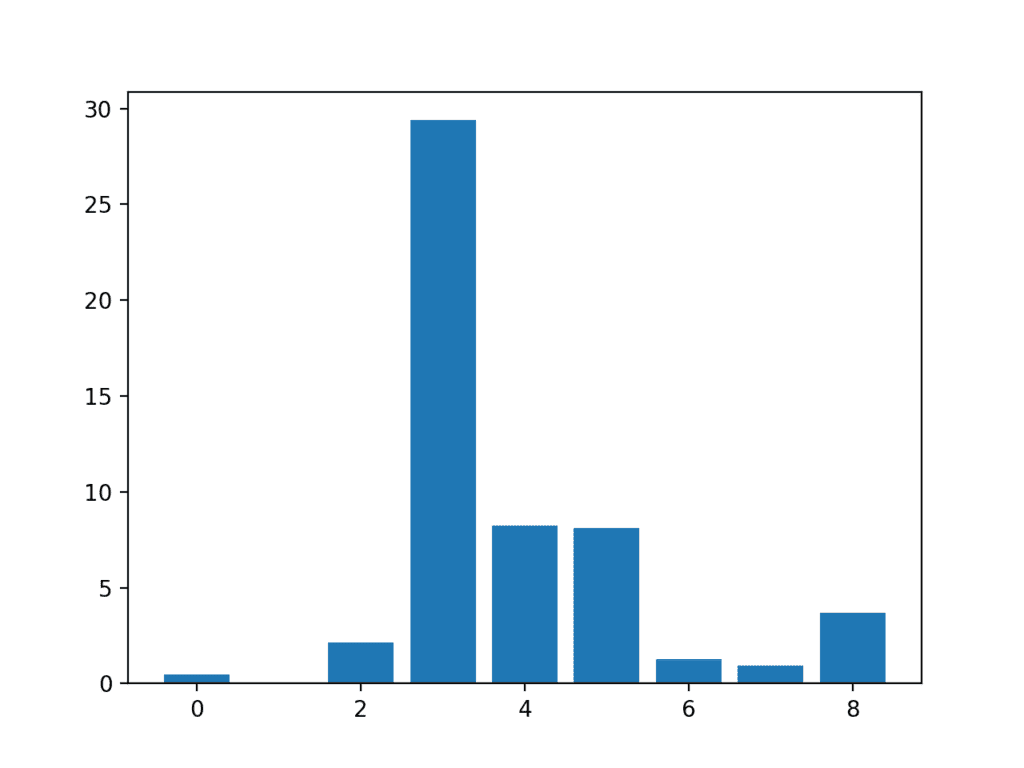
Bar Chart of the Input Features (x) vs The Chi-Squared Feature Importance (y)
Mutual Information Feature Selection
Mutual information from the field of information theory is the application of information gain (typically used in the construction of decision trees) to feature selection.
Mutual information is calculated between two variables and measures the reduction in uncertainty for one variable given a known value of the other variable.
You can learn more about mutual information in the following tutorial.
The scikit-learn machine learning library provides an implementation of mutual information for feature selection via the mutual_info_classif() function.
Like chi2(), it can be used in the SelectKBest feature selection strategy (and other strategies).
# feature selection def select_features(X_train, y_train, X_test): fs = SelectKBest(score_func=mutual_info_classif, k='all') fs.fit(X_train, y_train) X_train_fs = fs.transform(X_train) X_test_fs = fs.transform(X_test) return X_train_fs, X_test_fs, fs
We can perform feature selection using mutual information on the breast cancer set and print and plot the scores (larger is better) as we did in the previous section.
The complete example of using mutual information for categorical feature selection is listed below.
# example of mutual information feature selection for categorical data
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif
from matplotlib import pyplot
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# prepare input data
def prepare_inputs(X_train, X_test):
oe = OrdinalEncoder()
oe.fit(X_train)
X_train_enc = oe.transform(X_train)
X_test_enc = oe.transform(X_test)
return X_train_enc, X_test_enc
# prepare target
def prepare_targets(y_train, y_test):
le = LabelEncoder()
le.fit(y_train)
y_train_enc = le.transform(y_train)
y_test_enc = le.transform(y_test)
return y_train_enc, y_test_enc
# feature selection
def select_features(X_train, y_train, X_test):
fs = SelectKBest(score_func=mutual_info_classif, k='all')
fs.fit(X_train, y_train)
X_train_fs = fs.transform(X_train)
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# prepare input data
X_train_enc, X_test_enc = prepare_inputs(X_train, X_test)
# prepare output data
y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train_enc, y_train_enc, X_test_enc)
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
Running the example first prints the scores calculated for each input feature and the target variable.
Note: your specific results may differ. Try running the example a few times.
In this case, we can see that some of the features have a very low score, suggesting that perhaps they can be removed.
Perhaps features 3, 6, 2, and 5 are most relevant.
Feature 0: 0.003588 Feature 1: 0.000000 Feature 2: 0.025934 Feature 3: 0.071461 Feature 4: 0.000000 Feature 5: 0.038973 Feature 6: 0.064759 Feature 7: 0.003068 Feature 8: 0.000000
A bar chart of the feature importance scores for each input feature is created.
Importantly, a different mixture of features is promoted.
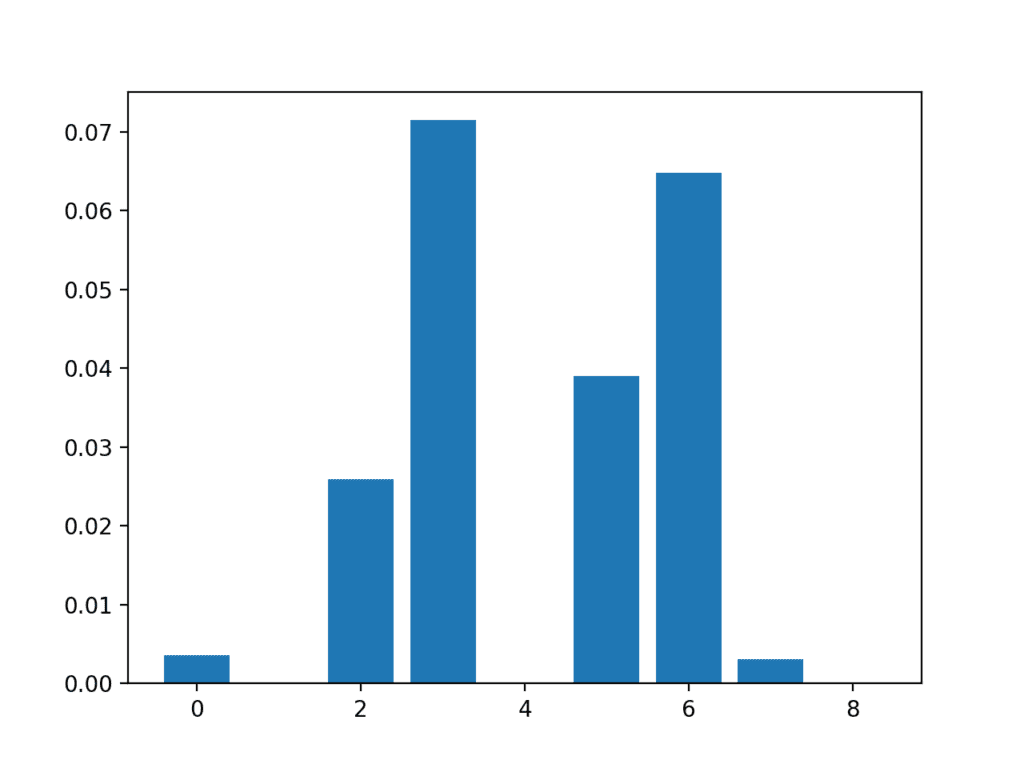
Bar Chart of the Input Features (x) vs The Mutual Information Feature Importance (y)
Now that we know how to perform feature selection on categorical data for a classification predictive modeling problem, we can try developing a model using the selected features and compare the results.
Modeling With Selected Features
There are many different techniques for scoring features and selecting features based on scores; how do you know which one to use?
A robust approach is to evaluate models using different feature selection methods (and numbers of features) and select the method that results in a model with the best performance.
In this section, we will evaluate a Logistic Regression model with all features compared to a model built from features selected by chi-squared and those features selected via mutual information.
Logistic regression is a good model for testing feature selection methods as it can perform better if irrelevant features are removed from the model.
Model Built Using All Features
As a first step, we will evaluate a LogisticRegression model using all the available features.
The model is fit on the training dataset and evaluated on the test dataset.
The complete example is listed below.
# evaluation of a model using all input features
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# prepare input data
def prepare_inputs(X_train, X_test):
oe = OrdinalEncoder()
oe.fit(X_train)
X_train_enc = oe.transform(X_train)
X_test_enc = oe.transform(X_test)
return X_train_enc, X_test_enc
# prepare target
def prepare_targets(y_train, y_test):
le = LabelEncoder()
le.fit(y_train)
y_train_enc = le.transform(y_train)
y_test_enc = le.transform(y_test)
return y_train_enc, y_test_enc
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# prepare input data
X_train_enc, X_test_enc = prepare_inputs(X_train, X_test)
# prepare output data
y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
# fit the model
model = LogisticRegression(solver='lbfgs')
model.fit(X_train_enc, y_train_enc)
# evaluate the model
yhat = model.predict(X_test_enc)
# evaluate predictions
accuracy = accuracy_score(y_test_enc, yhat)
print('Accuracy: %.2f' % (accuracy*100))
Running the example prints the accuracy of the model on the training dataset.
Note: your specific results may vary given the stochastic nature of the learning algorithm. Try running the example a few times.
In this case, we can see that the model achieves a classification accuracy of about 75%.
We would prefer to use a subset of features that achieves a classification accuracy that is as good or better than this.
Accuracy: 75.79
Model Built Using Chi-Squared Features
We can use the chi-squared test to score the features and select the four most relevant features.
The select_features() function below is updated to achieve this.
# feature selection def select_features(X_train, y_train, X_test): fs = SelectKBest(score_func=chi2, k=4) fs.fit(X_train, y_train) X_train_fs = fs.transform(X_train) X_test_fs = fs.transform(X_test) return X_train_fs, X_test_fs
The complete example of evaluating a logistic regression model fit and evaluated on data using this feature selection method is listed below.
# evaluation of a model fit using chi squared input features
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# prepare input data
def prepare_inputs(X_train, X_test):
oe = OrdinalEncoder()
oe.fit(X_train)
X_train_enc = oe.transform(X_train)
X_test_enc = oe.transform(X_test)
return X_train_enc, X_test_enc
# prepare target
def prepare_targets(y_train, y_test):
le = LabelEncoder()
le.fit(y_train)
y_train_enc = le.transform(y_train)
y_test_enc = le.transform(y_test)
return y_train_enc, y_test_enc
# feature selection
def select_features(X_train, y_train, X_test):
fs = SelectKBest(score_func=chi2, k=4)
fs.fit(X_train, y_train)
X_train_fs = fs.transform(X_train)
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# prepare input data
X_train_enc, X_test_enc = prepare_inputs(X_train, X_test)
# prepare output data
y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
# feature selection
X_train_fs, X_test_fs = select_features(X_train_enc, y_train_enc, X_test_enc)
# fit the model
model = LogisticRegression(solver='lbfgs')
model.fit(X_train_fs, y_train_enc)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
accuracy = accuracy_score(y_test_enc, yhat)
print('Accuracy: %.2f' % (accuracy*100))
Running the example reports the performance of the model on just four of the nine input features selected using the chi-squared statistic.
Note: your specific results may vary given the stochastic nature of the learning algorithm. Try running the example a few times.
In this case, we see that the model achieved an accuracy of about 74%, a slight drop in performance.
It is possible that some of the features removed are, in fact, adding value directly or in concert with the selected features.
At this stage, we would probably prefer to use all of the input features.
Accuracy: 74.74
Model Built Using Mutual Information Features
We can repeat the experiment and select the top four features using a mutual information statistic.
The updated version of the select_features() function to achieve this is listed below.
# feature selection def select_features(X_train, y_train, X_test): fs = SelectKBest(score_func=mutual_info_classif, k=4) fs.fit(X_train, y_train) X_train_fs = fs.transform(X_train) X_test_fs = fs.transform(X_test) return X_train_fs, X_test_fs
The complete example of using mutual information for feature selection to fit a logistic regression model is listed below.
# evaluation of a model fit using mutual information input features
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# load the dataset
def load_dataset(filename):
# load the dataset as a pandas DataFrame
data = read_csv(filename, header=None)
# retrieve numpy array
dataset = data.values
# split into input (X) and output (y) variables
X = dataset[:, :-1]
y = dataset[:,-1]
# format all fields as string
X = X.astype(str)
return X, y
# prepare input data
def prepare_inputs(X_train, X_test):
oe = OrdinalEncoder()
oe.fit(X_train)
X_train_enc = oe.transform(X_train)
X_test_enc = oe.transform(X_test)
return X_train_enc, X_test_enc
# prepare target
def prepare_targets(y_train, y_test):
le = LabelEncoder()
le.fit(y_train)
y_train_enc = le.transform(y_train)
y_test_enc = le.transform(y_test)
return y_train_enc, y_test_enc
# feature selection
def select_features(X_train, y_train, X_test):
fs = SelectKBest(score_func=mutual_info_classif, k=4)
fs.fit(X_train, y_train)
X_train_fs = fs.transform(X_train)
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs
# load the dataset
X, y = load_dataset('breast-cancer.csv')
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# prepare input data
X_train_enc, X_test_enc = prepare_inputs(X_train, X_test)
# prepare output data
y_train_enc, y_test_enc = prepare_targets(y_train, y_test)
# feature selection
X_train_fs, X_test_fs = select_features(X_train_enc, y_train_enc, X_test_enc)
# fit the model
model = LogisticRegression(solver='lbfgs')
model.fit(X_train_fs, y_train_enc)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
accuracy = accuracy_score(y_test_enc, yhat)
print('Accuracy: %.2f' % (accuracy*100))
Running the example fits the model on the four top selected features chosen using mutual information.
Note: your specific results may vary given the stochastic nature of the learning algorithm. Try running the example a few times.
In this case, we can see a small lift in classification accuracy to 76%.
To be sure that the effect is real, it would be a good idea to repeat each experiment multiple times and compare the mean performance. It may also be a good idea to explore using k-fold cross-validation instead of a simple train/test split.
Accuracy: 76.84
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Posts
- A Gentle Introduction to the Chi-Squared Test for Machine Learning
- An Introduction to Feature Selection
- Feature Selection For Machine Learning in Python
- What is Information Gain and Mutual Information for Machine Learning
API
- sklearn.model_selection.train_test_split API.
- sklearn.preprocessing.OrdinalEncoder API.
- sklearn.preprocessing.LabelEncoder API.
- sklearn.feature_selection.chi2 API
- sklearn.feature_selection.SelectKBest API
- sklearn.feature_selection.mutual_info_classif API.
- sklearn.linear_model.LogisticRegression API.
Articles
- Breast Cancer Data Set, UCI Machine Learning Repository.
- Breast Cancer Raw Dataset
- Breast Cancer Description
Summary
In this tutorial, you discovered how to perform feature selection with categorical input data.
Specifically, you learned:
- The breast cancer predictive modeling problem with categorical inputs and binary classification target variable.
- How to evaluate the importance of categorical features using the chi-squared and mutual information statistics.
- How to perform feature selection for categorical data when fitting and evaluating a classification model.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post How to Perform Feature Selection with Categorical Data appeared first on Machine Learning Mastery.
