Author: Jason Brownlee
Cancer detection is a popular example of an imbalanced classification problem because there are often significantly more cases of non-cancer than actual cancer.
A standard imbalanced classification dataset is the mammography dataset that involves detecting breast cancer from radiological scans, specifically the presence of clusters of microcalcifications that appear bright on a mammogram. This dataset was constructed by scanning the images, segmenting them into candidate objects, and using computer vision techniques to describe each candidate object.
It is a popular dataset for imbalanced classification because of the severe class imbalance, specifically where 98 percent of candidate microcalcifications are not cancer and only 2 percent were labeled as cancer by an experienced radiographer.
In this tutorial, you will discover how to develop and evaluate models for the imbalanced mammography cancer classification dataset.
After completing this tutorial, you will know:
- How to load and explore the dataset and generate ideas for data preparation and model selection.
- How to evaluate a suite of machine learning models and improve their performance with data cost-sensitive techniques.
- How to fit a final model and use it to predict class labels for specific cases.
Discover SMOTE, one-class classification, cost-sensitive learning, threshold moving, and much more in my new book, with 30 step-by-step tutorials and full Python source code.
Let’s get started.

Develop an Imbalanced Classification Model to Detect Microcalcifications
Photo by Bernard Spragg. NZ, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
- Mammography Dataset
- Explore the Dataset
- Model Test and Baseline Result
- Evaluate Models
- Evaluate Machine Learning Algorithms
- Evaluate Cost-Sensitive Algorithms
- Make Predictions on New Data
Mammography Dataset
In this project, we will use a standard imbalanced machine learning dataset referred to as the “mammography” dataset or sometimes “Woods Mammography.”
The dataset is credited to Kevin Woods, et al. and the 1993 paper titled “Comparative Evaluation Of Pattern Recognition Techniques For Detection Of Microcalcifications In Mammography.”
The focus of the problem is on detecting breast cancer from radiological scans, specifically the presence of clusters of microcalcifications that appear bright on a mammogram.
The dataset involved first started with 24 mammograms with a known cancer diagnosis that were scanned. The images were then pre-processed using image segmentation computer vision algorithms to extract candidate objects from the mammogram images. Once segmented, the objects were then manually labeled by an experienced radiologist.
A total of 29 features were extracted from the segmented objects thought to be most relevant to pattern recognition, which was reduced to 18, then finally to seven, as follows (taken directly from the paper):
- Area of object (in pixels).
- Average gray level of the object.
- Gradient strength of the object’s perimeter pixels.
- Root mean square noise fluctuation in the object.
- Contrast, average gray level of the object minus the average of a two-pixel wide border surrounding the object.
- A low order moment based on shape descriptor.
There are two classes and the goal is to distinguish between microcalcifications and non-microcalcifications using the features for a given segmented object.
- Non-microcalcifications: negative case, or majority class.
- Microcalcifications: positive case, or minority class.
A number of models were evaluated and compared in the original paper, such as neural networks, decision trees, and k-nearest neighbors. Models were evaluated using ROC Curves and compared using the area under ROC Curve, or ROC AUC for short.
ROC Curves and area under ROC Curves were chosen with the intent to minimize the false-positive rate (complement of the specificity) and maximize the true-positive rate (sensitivity), the two axes of the ROC Curve. The use of the ROC Curves also suggests the desire for a probabilistic model from which an operator can select a probability threshold as the cut-off between the acceptable false positive and true positive rates.
Their results suggested a “linear classifier” (seemingly a Gaussian Naive Bayes classifier) performed the best with a ROC AUC of 0.936 averaged over 100 runs.
Next, let’s take a closer look at the data.
Want to Get Started With Imbalance Classification?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Explore the Dataset
The Mammography dataset is a widely used standard machine learning dataset, used to explore and demonstrate many techniques designed specifically for imbalanced classification.
One example is the popular SMOTE data oversampling technique.
A version of this dataset was made available that has some differences to the dataset described in the original paper.
First, download the dataset and save it in your current working directory with the name “mammography.csv”
Review the contents of the file.
The first few lines of the file should look as follows:
0.23001961,5.0725783,-0.27606055,0.83244412,-0.37786573,0.4803223,'-1' 0.15549112,-0.16939038,0.67065219,-0.85955255,-0.37786573,-0.94572324,'-1' -0.78441482,-0.44365372,5.6747053,-0.85955255,-0.37786573,-0.94572324,'-1' 0.54608818,0.13141457,-0.45638679,-0.85955255,-0.37786573,-0.94572324,'-1' -0.10298725,-0.3949941,-0.14081588,0.97970269,-0.37786573,1.0135658,'-1' ...
We can see that the dataset has six rather than the seven input variables. It is possible that the first input variable listed in the paper (area in pixels) was removed from this version of the dataset.
The input variables are numerical (real-valued) and the target variable is the string with ‘-1’ for the majority class and ‘1’ for the minority class. These values will need to be encoded as 0 and 1 respectively to meet the expectations of classification algorithms on binary imbalanced classification problems.
The dataset can be loaded as a DataFrame using the read_csv() Pandas function, specifying the location and the fact that there is no header line.
... # define the dataset location filename = 'mammography.csv' # load the csv file as a data frame dataframe = read_csv(filename, header=None)
Once loaded, we can summarize the number of rows and columns by printing the shape of the DataFrame.
... # summarize the shape of the dataset print(dataframe.shape)
We can also summarize the number of examples in each class using the Counter object.
...
# summarize the class distribution
target = dataframe.values[:,-1]
counter = Counter(target)
for k,v in counter.items():
per = v / len(target) * 100
print('Class=%s, Count=%d, Percentage=%.3f%%' % (k, v, per))
Tying this together, the complete example of loading and summarizing the dataset is listed below.
# load and summarize the dataset
from pandas import read_csv
from collections import Counter
# define the dataset location
filename = 'mammography.csv'
# load the csv file as a data frame
dataframe = read_csv(filename, header=None)
# summarize the shape of the dataset
print(dataframe.shape)
# summarize the class distribution
target = dataframe.values[:,-1]
counter = Counter(target)
for k,v in counter.items():
per = v / len(target) * 100
print('Class=%s, Count=%d, Percentage=%.3f%%' % (k, v, per))
Running the example first loads the dataset and confirms the number of rows and columns, that is 11,183 rows and six input variables and one target variable.
The class distribution is then summarized, confirming the severe class imbalanced with approximately 98 percent for the majority class (no cancer) and approximately 2 percent for the minority class (cancer).
(11183, 7) Class='-1', Count=10923, Percentage=97.675% Class='1', Count=260, Percentage=2.325%
The dataset appears to generally match the dataset described in the SMOTE paper. Specifically in terms of the ratio of negative to positive examples.
A typical mammography dataset might contain 98% normal pixels and 2% abnormal pixels.
— SMOTE: Synthetic Minority Over-sampling Technique, 2002.
Also, the specific number of examples in the minority and majority classes also matches the paper.
The experiments were conducted on the mammography dataset. There were 10923 examples in the majority class and 260 examples in the minority class originally.
— SMOTE: Synthetic Minority Over-sampling Technique, 2002.
I believe this is the same dataset, although I cannot explain the mismatch in the number of input features, e.g. six compared to seven in the original paper.
We can also take a look at the distribution of the six numerical input variables by creating a histogram for each.
The complete example is listed below.
# create histograms of numeric input variables from pandas import read_csv from matplotlib import pyplot # define the dataset location filename = 'mammography.csv' # load the csv file as a data frame df = read_csv(filename, header=None) # histograms of all variables df.hist() pyplot.show()
Running the example creates the figure with one histogram subplot for each of the six numerical input variables in the dataset.
We can see that the variables have differing scales and that most of the variables have an exponential distribution, e.g. most cases falling into one bin, and the rest falling into a long tail. The final variable appears to have a bimodal distribution.
Depending on the choice of modeling algorithms, we would expect scaling the distributions to the same range to be useful, and perhaps the use of some power transforms.
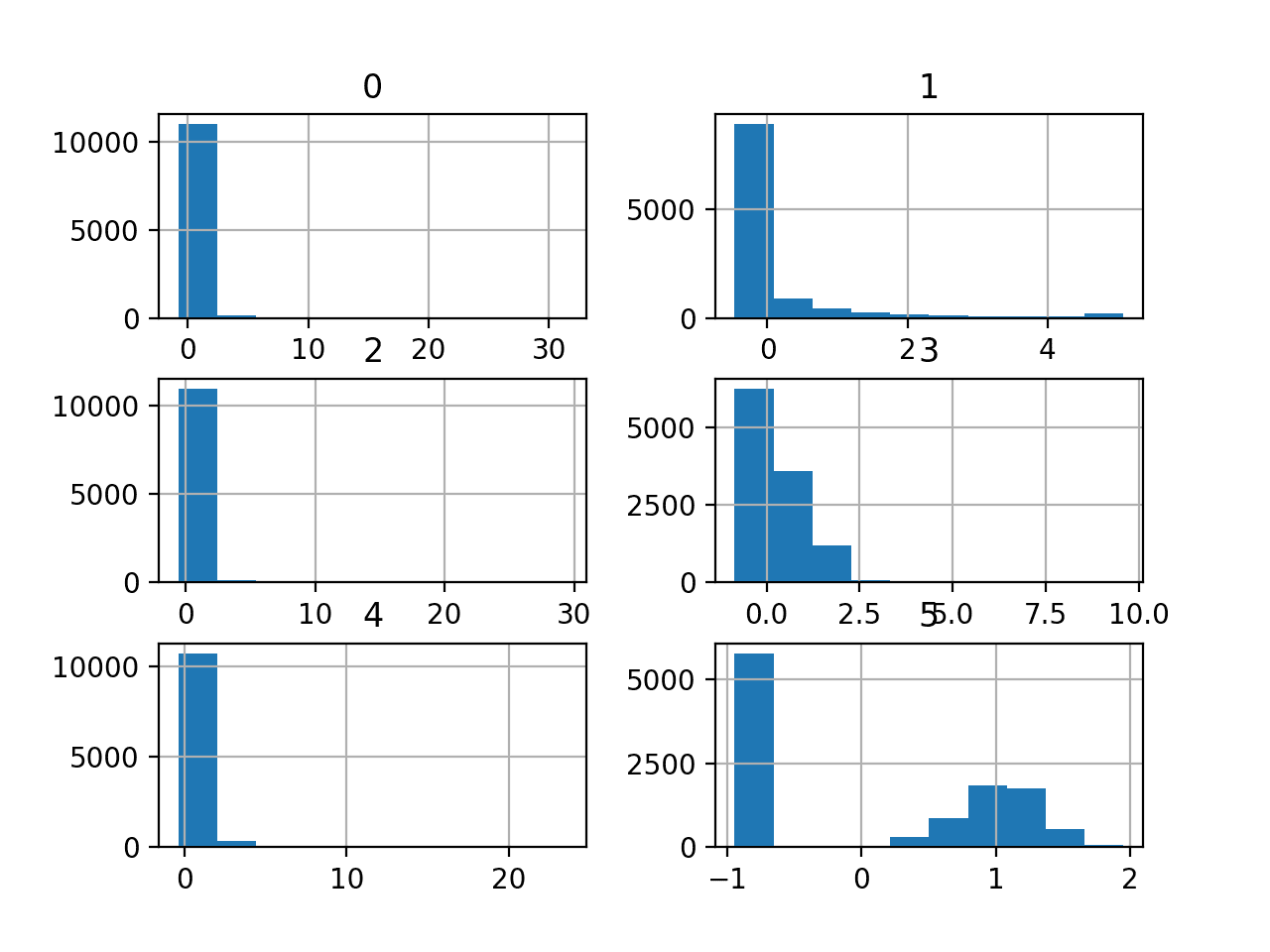
Histogram Plots of the Numerical Input Variables for the Mammography Dataset
We can also create a scatter plot for each pair of input variables, called a scatter plot matrix.
This can be helpful to see if any variables relate to each other or change in the same direction, e.g. are correlated.
We can also color the dots of each scatter plot according to the class label. In this case, the majority class (no cancer) will be mapped to blue dots and the minority class (cancer) will be mapped to red dots.
The complete example is listed below.
# create pairwise scatter plots of numeric input variables
from pandas import read_csv
from pandas.plotting import scatter_matrix
from matplotlib import pyplot
# define the dataset location
filename = 'mammography.csv'
# load the csv file as a data frame
df = read_csv(filename, header=None)
# define a mapping of class values to colors
color_dict = {"'-1'":'blue', "'1'":'red'}
# map each row to a color based on the class value
colors = [color_dict[str(x)] for x in df.values[:, -1]]
# pairwise scatter plots of all numerical variables
scatter_matrix(df, diagonal='kde', color=colors)
pyplot.show()
Running the example creates a figure showing the scatter plot matrix, with six plots by six plots, comparing each of the six numerical input variables with each other. The diagonal of the matrix shows the density distribution of each variable.
Each pairing appears twice both above and below the top-left to bottom-right diagonal, providing two ways to review the same variable interactions.
We can see that the distributions for many variables do differ for the two-class labels, suggesting that some reasonable discrimination between the cancer and no cancer cases will be feasible.
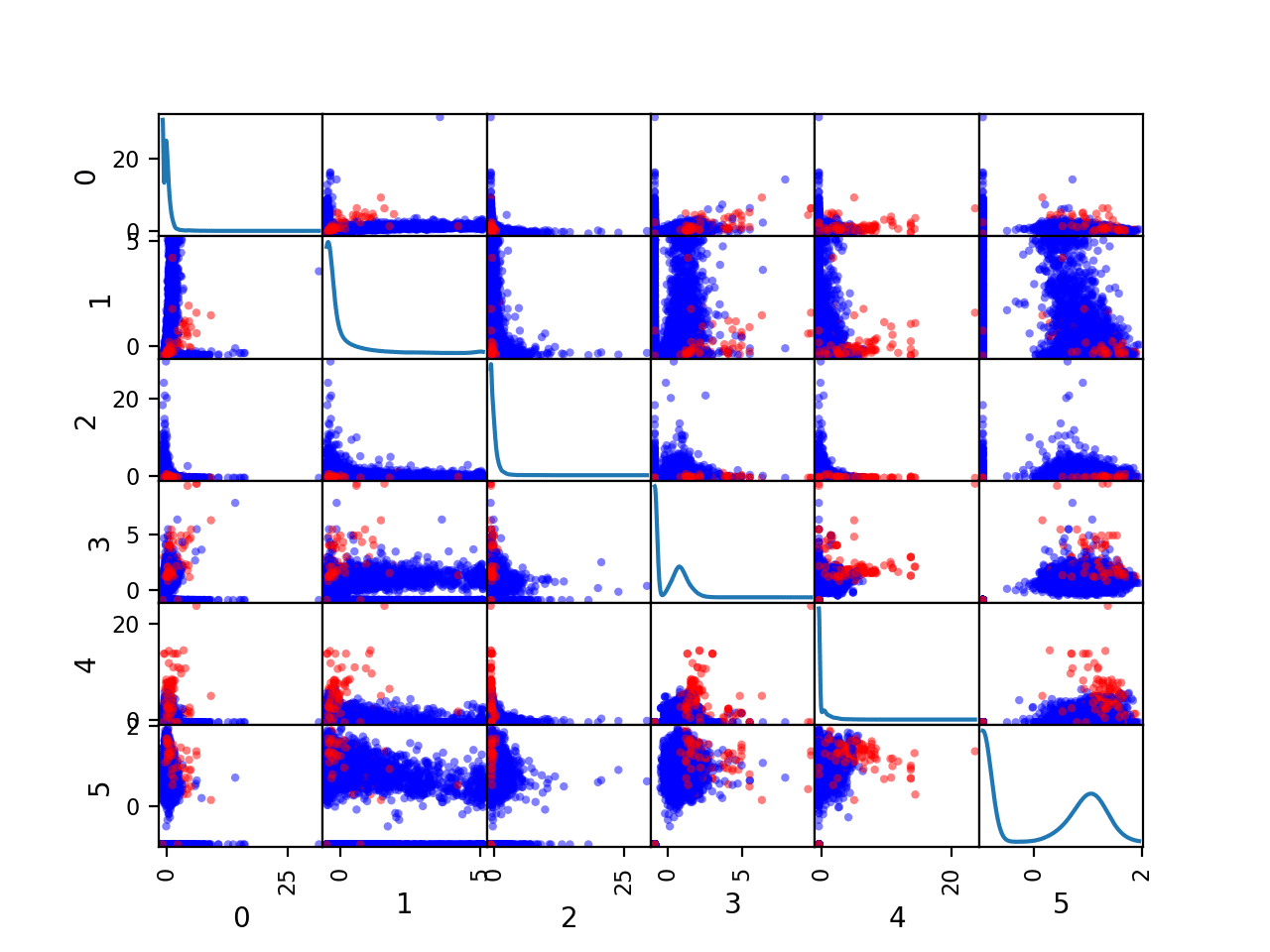
Scatter Plot Matrix by Class for the Numerical Input Variables in the Mammography Dataset
Now that we have reviewed the dataset, let’s look at developing a test harness for evaluating candidate models.
Model Test and Baseline Result
We will evaluate candidate models using repeated stratified k-fold cross-validation.
The k-fold cross-validation procedure provides a good general estimate of model performance that is not too optimistically biased, at least compared to a single train-test split. We will use k=10, meaning each fold will contain about 11183/10 or about 1,118 examples.
Stratified means that each fold will contain the same mixture of examples by class, that is about 98 percent to 2 percent no-cancer to cancer objects. Repetition indicates that the evaluation process will be performed multiple times to help avoid fluke results and better capture the variance of the chosen model. We will use three repeats.
This means a single model will be fit and evaluated 10 * 3 or 30 times and the mean and standard deviation of these runs will be reported.
This can be achieved using the RepeatedStratifiedKFold scikit-learn class.
We will evaluate and compare models using the area under ROC Curve or ROC AUC calculated via the roc_auc_score() function.
We can define a function to load the dataset and split the columns into input and output variables. We will correctly encode the class labels as 0 and 1. The load_dataset() function below implements this.
# load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, :-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y
We can then define a function that will evaluate a given model on the dataset and return a list of ROC AUC scores for each fold and repeat.
The evaluate_model() function below implements this, taking the dataset and model as arguments and returning the list of scores.
# evaluate a model def evaluate_model(X, y, model): # define evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # evaluate model scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1) return scores
Finally, we can evaluate a baseline model on the dataset using this test harness.
A model that predicts the a random class in proportion to the base rate of each class will result in a ROC AUC of 0.5, the baseline in performance on this dataset. This is a so-called “no skill” classifier.
This can be achieved using the DummyClassifier class from the scikit-learn library and setting the “strategy” argument to ‘stratified‘.
... # define the reference model model = DummyClassifier(strategy='stratified')
Once the model is evaluated, we can report the mean and standard deviation of the ROC AUC scores directly.
...
# evaluate the model
scores = evaluate_model(X, y, model)
# summarize performance
print('Mean ROC AUC: %.3f (%.3f)' % (mean(scores), std(scores)))
Tying this together, the complete example of loading the dataset, evaluating a baseline model, and reporting the performance is listed below.
# test harness and baseline model evaluation
from collections import Counter
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.dummy import DummyClassifier
# load the dataset
def load_dataset(full_path):
# load the dataset as a numpy array
data = read_csv(full_path, header=None)
# retrieve numpy array
data = data.values
# split into input and output elements
X, y = data[:, :-1], data[:, -1]
# label encode the target variable to have the classes 0 and 1
y = LabelEncoder().fit_transform(y)
return X, y
# evaluate a model
def evaluate_model(X, y, model):
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)
return scores
# define the location of the dataset
full_path = 'mammography.csv'
# load the dataset
X, y = load_dataset(full_path)
# summarize the loaded dataset
print(X.shape, y.shape, Counter(y))
# define the reference model
model = DummyClassifier(strategy='stratified')
# evaluate the model
scores = evaluate_model(X, y, model)
# summarize performance
print('Mean ROC AUC: %.3f (%.3f)' % (mean(scores), std(scores)))
Running the example first loads and summarizes the dataset.
We can see that we have the correct number of rows loaded, and that we have six computer vision derived input variables. Importantly, we can see that the class labels have the correct mapping to integers with 0 for the majority class and 1 for the minority class, customary for imbalanced binary classification datasets.
Next, the average of the ROC AUC scores is reported.
As expected, the no-skill classifier achieves the worst-case performance of a mean ROC AUC of approximately 0.5. This provides a baseline in performance, above which a model can be considered skillful on this dataset.
(11183, 6) (11183,) Counter({0: 10923, 1: 260})
Mean ROC AUC: 0.503 (0.016)
Now that we have a test harness and a baseline in performance, we can begin to evaluate some models on this dataset.
Evaluate Models
In this section, we will evaluate a suite of different techniques on the dataset using the test harness developed in the previous section.
The goal is to both demonstrate how to work through the problem systematically and to demonstrate the capability of some techniques designed for imbalanced classification problems.
The reported performance is good, but not highly optimized (e.g. hyperparameters are not tuned).
Can you do better? If you can achieve better ROC AUC performance using the same test harness, I’d love to hear about it. Let me know in the comments below.
Evaluate Machine Learning Algorithms
Let’s start by evaluating a mixture of machine learning models on the dataset.
It can be a good idea to spot check a suite of different linear and nonlinear algorithms on a dataset to quickly flush out what works well and deserves further attention, and what doesn’t.
We will evaluate the following machine learning models on the mammography dataset:
- Logistic Regression (LR)
- Support Vector Machine (SVM)
- Bagged Decision Trees (BAG)
- Random Forest (RF)
- Gradient Boosting Machine (GBM)
We will use mostly default model hyperparameters, with the exception of the number of trees in the ensemble algorithms, which we will set to a reasonable default of 1,000.
We will define each model in turn and add them to a list so that we can evaluate them sequentially. The get_models() function below defines the list of models for evaluation, as well as a list of model short names for plotting the results later.
# define models to test
def get_models():
models, names = list(), list()
# LR
models.append(LogisticRegression(solver='lbfgs'))
names.append('LR')
# SVM
models.append(SVC(gamma='scale'))
names.append('SVM')
# Bagging
models.append(BaggingClassifier(n_estimators=1000))
names.append('BAG')
# RF
models.append(RandomForestClassifier(n_estimators=1000))
names.append('RF')
# GBM
models.append(GradientBoostingClassifier(n_estimators=1000))
names.append('GBM')
return models, names
We can then enumerate the list of models in turn and evaluate each, reporting the mean ROC AUC and storing the scores for later plotting.
...
# define models
models, names = get_models()
results = list()
# evaluate each model
for i in range(len(models)):
# evaluate the model and store results
scores = evaluate_model(X, y, models[i])
results.append(scores)
# summarize and store
print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores)))
At the end of the run, we can plot each sample of scores as a box and whisker plot with the same scale so that we can directly compare the distributions.
... # plot the results pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show()
Tying this all together, the complete example of evaluating a suite of machine learning algorithms on the mammography dataset is listed below.
# spot check machine learning algorithms on the mammography dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from matplotlib import pyplot
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import BaggingClassifier
# load the dataset
def load_dataset(full_path):
# load the dataset as a numpy array
data = read_csv(full_path, header=None)
# retrieve numpy array
data = data.values
# split into input and output elements
X, y = data[:, :-1], data[:, -1]
# label encode the target variable to have the classes 0 and 1
y = LabelEncoder().fit_transform(y)
return X, y
# evaluate a model
def evaluate_model(X, y, model):
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)
return scores
# define models to test
def get_models():
models, names = list(), list()
# LR
models.append(LogisticRegression(solver='lbfgs'))
names.append('LR')
# SVM
models.append(SVC(gamma='scale'))
names.append('SVM')
# Bagging
models.append(BaggingClassifier(n_estimators=1000))
names.append('BAG')
# RF
models.append(RandomForestClassifier(n_estimators=1000))
names.append('RF')
# GBM
models.append(GradientBoostingClassifier(n_estimators=1000))
names.append('GBM')
return models, names
# define the location of the dataset
full_path = 'mammography.csv'
# load the dataset
X, y = load_dataset(full_path)
# define models
models, names = get_models()
results = list()
# evaluate each model
for i in range(len(models)):
# evaluate the model and store results
scores = evaluate_model(X, y, models[i])
results.append(scores)
# summarize and store
print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores)))
# plot the results
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()
Running the example evaluates each algorithm in turn and reports the mean and standard deviation ROC AUC.
Your specific results will vary given the stochastic nature of the learning algorithms; consider running the example a few times.
In this case, we can see that all of the tested algorithms have skill, achieving a ROC AUC above the default of 0.5.
The results suggest that the ensemble of decision tree algorithms performs better on this dataset with perhaps Random Forest performing the best, with a ROC AUC of about 0.950.
It is interesting to note that this is better than the ROC AUC described in the paper of 0.93, although we used a different model evaluation procedure.
The evaluation was a little unfair to the LR and SVM algorithms as we did not scale the input variables prior to fitting the model. We can explore this in the next section.
>LR 0.919 (0.040) >SVM 0.880 (0.049) >BAG 0.941 (0.041) >RF 0.950 (0.036) >GBM 0.918 (0.037)
A figure is created showing one box and whisker plot for each algorithm’s sample of results. The box shows the middle 50 percent of the data, the orange line in the middle of each box shows the median of the sample, and the green triangle in each box shows the mean of the sample.
We can see that both BAG and RF have a tight distribution and a mean and median that closely align, perhaps suggesting a non-skewed and Gaussian distribution of scores, e.g. stable.
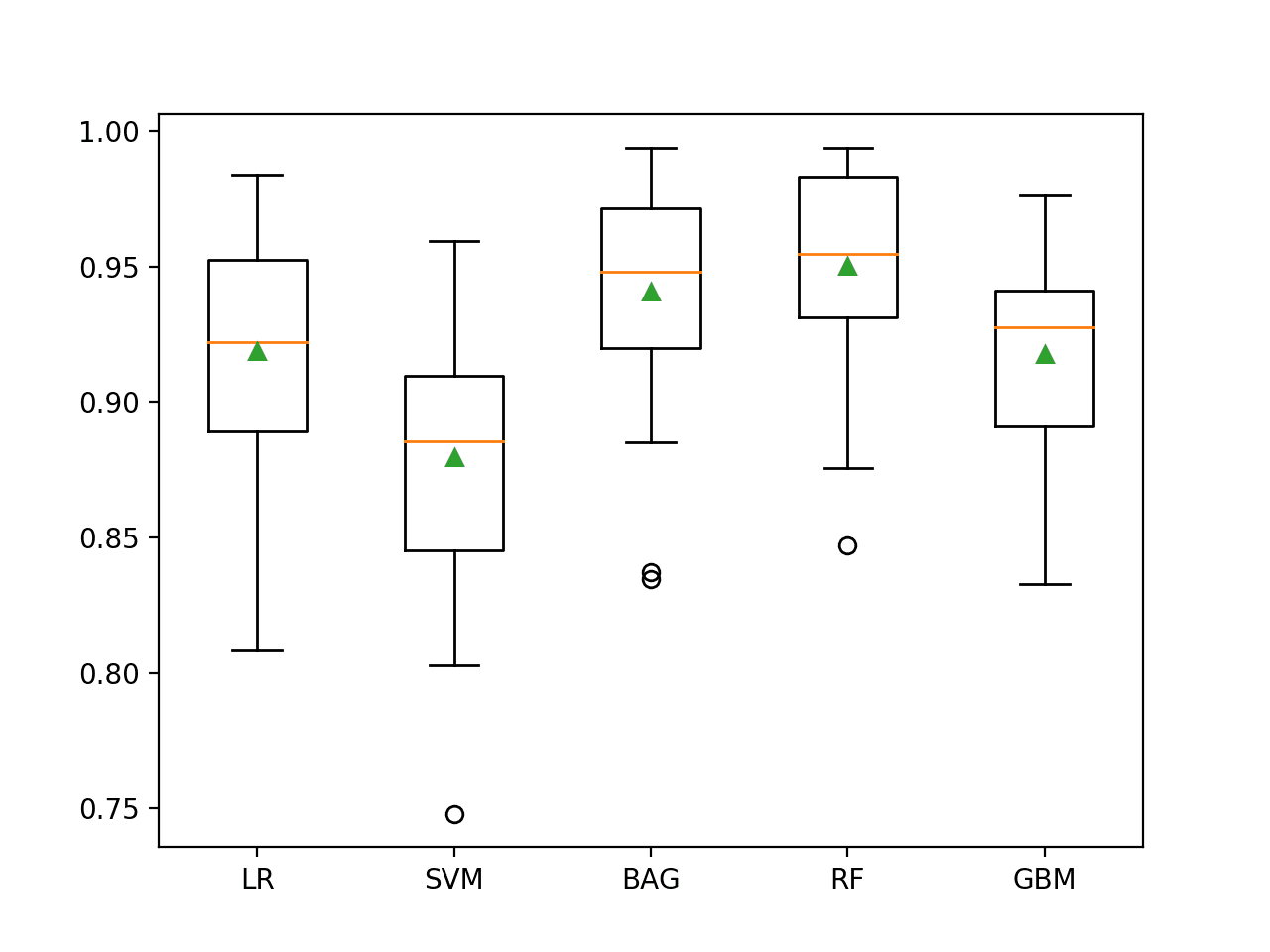
Box and Whisker Plot of Machine Learning Models on the Imbalanced Mammography Dataset
Now that we have a good first set of results, let’s see if we can improve them with cost-sensitive classifiers.
Evaluate Cost-Sensitive Algorithms
Some machine learning algorithms can be adapted to pay more attention to one class than another when fitting the model.
These are referred to as cost-sensitive machine learning models and they can be used for imbalanced classification by specifying a cost that is inversely proportional to the class distribution. For example, with a 98 percent to 2 percent distribution for the majority and minority classes, we can specify to give errors on the minority class a weighting of 98 and errors for the majority class a weighting of 2.
Three algorithms that offer this capability are:
- Logistic Regression (LR)
- Support Vector Machine (SVM)
- Random Forest (RF)
This can be achieved in scikit-learn by setting the “class_weight” argument to “balanced” to make these algorithms cost-sensitive.
For example, the updated get_models() function below defines the cost-sensitive version of these three algorithms to be evaluated on our dataset.
# define models to test
def get_models():
models, names = list(), list()
# LR
models.append(LogisticRegression(solver='lbfgs', class_weight='balanced'))
names.append('LR')
# SVM
models.append(SVC(gamma='scale', class_weight='balanced'))
names.append('SVM')
# RF
models.append(RandomForestClassifier(n_estimators=1000))
names.append('RF')
return models, names
Additionally, when exploring the dataset, we noticed that many of the variables had a seemingly exponential data distribution. Sometimes we can better spread the data for a variable by using a power transform on each variable. This will be particularly helpful to the LR and SVM algorithm and may also help the RF algorithm.
We can implement this within each fold of the cross-validation model evaluation process using a Pipeline. The first step will learn the PowerTransformer on the training set folds and apply it to the training and test set folds. The second step will be the model that we are evaluating. The pipeline can then be evaluated directly using our evaluate_model() function, for example:
...
# defines pipeline steps
steps = [('p', PowerTransformer()), ('m',models[i])]
# define pipeline
pipeline = Pipeline(steps=steps)
# evaluate the pipeline and store results
scores = evaluate_model(X, y, pipeline)
Tying this together, the complete example of evaluating power transformed cost-sensitive machine learning algorithms on the mammography dataset is listed below.
# cost-sensitive machine learning algorithms on the mammography dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from matplotlib import pyplot
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import PowerTransformer
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
# load the dataset
def load_dataset(full_path):
# load the dataset as a numpy array
data = read_csv(full_path, header=None)
# retrieve numpy array
data = data.values
# split into input and output elements
X, y = data[:, :-1], data[:, -1]
# label encode the target variable to have the classes 0 and 1
y = LabelEncoder().fit_transform(y)
return X, y
# evaluate a model
def evaluate_model(X, y, model):
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)
return scores
# define models to test
def get_models():
models, names = list(), list()
# LR
models.append(LogisticRegression(solver='lbfgs', class_weight='balanced'))
names.append('LR')
# SVM
models.append(SVC(gamma='scale', class_weight='balanced'))
names.append('SVM')
# RF
models.append(RandomForestClassifier(n_estimators=1000))
names.append('RF')
return models, names
# define the location of the dataset
full_path = 'mammography.csv'
# load the dataset
X, y = load_dataset(full_path)
# define models
models, names = get_models()
results = list()
# evaluate each model
for i in range(len(models)):
# defines pipeline steps
steps = [('p', PowerTransformer()), ('m',models[i])]
# define pipeline
pipeline = Pipeline(steps=steps)
# evaluate the pipeline and store results
scores = evaluate_model(X, y, pipeline)
results.append(scores)
# summarize and store
print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores)))
# plot the results
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()
Running the example evaluates each algorithm in turn and reports the mean and standard deviation ROC AUC.
Your specific results will vary given the stochastic nature of the learning algorithms; consider running the example a few times.
In this case, we can see that all three of the tested algorithms achieved a lift on ROC AUC compared to their non-transformed and cost-insensitive versions. It would be interesting to repeat the experiment without the transform to see if it was the transform or the cost-sensitive version of the algorithms, or both that resulted in the lifts in performance.
In this case, we can see the SVM achieved the best performance, performing better than RF in this and the previous section and achieving a mean ROC AUC of about 0.957.
>LR 0.922 (0.036) >SVM 0.957 (0.024) >RF 0.951 (0.035)
Box and whisker plots are then created comparing the distribution of ROC AUC scores.
The SVM distribution appears compact compared to the other two models. As such the performance is likely stable and may make a good choice for a final model.
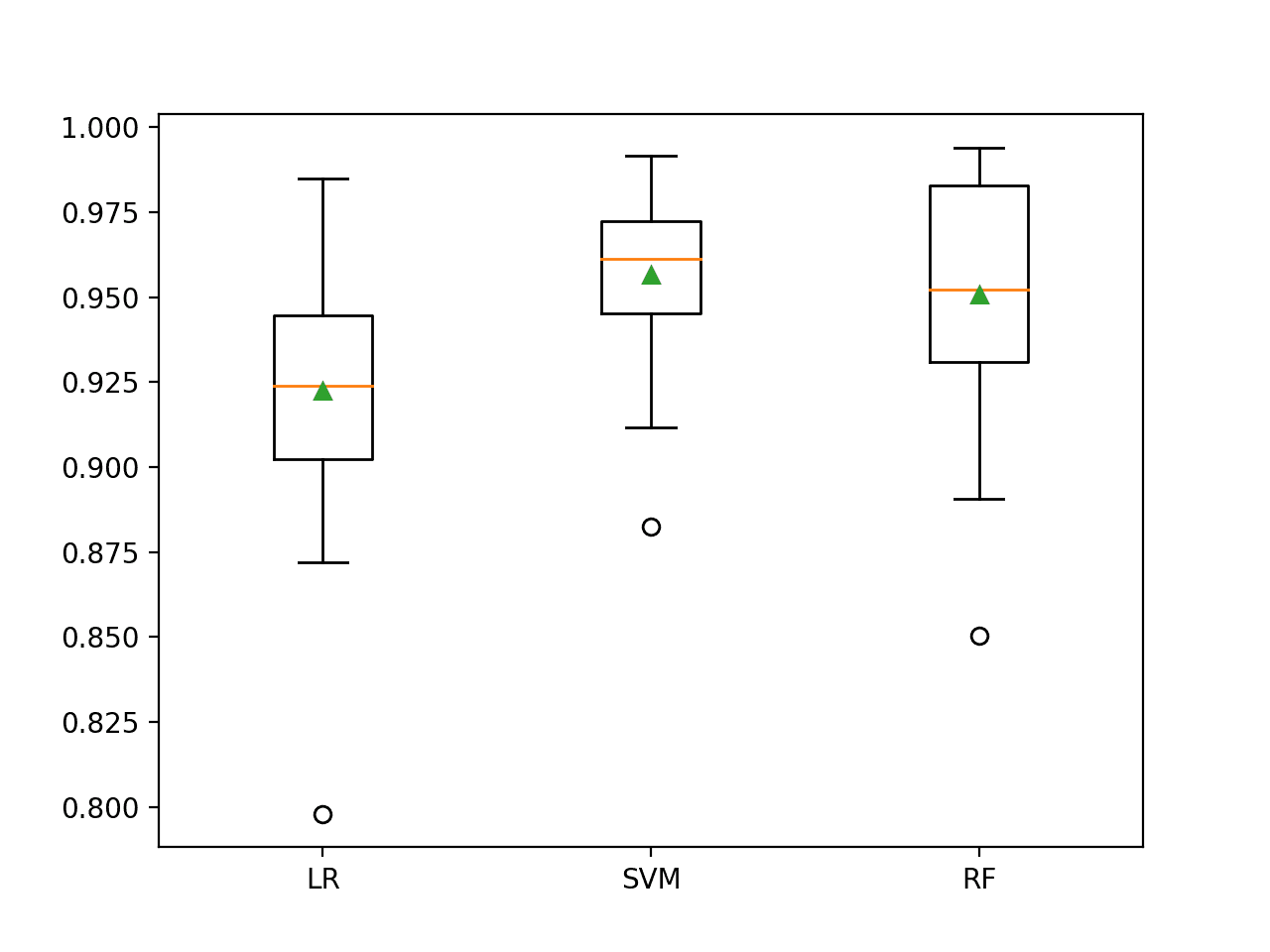
Box and Whisker Plots of Cost-Sensitive Machine Learning Models on the Imbalanced Mammography Dataset
Next, let’s see how we might use a final model to make predictions on new data.
Make Predictions on New Data
In this section, we will fit a final model and use it to make predictions on single rows of data
We will use the cost-sensitive version of the SVM model as the final model and a power transform on the data prior to fitting the model and making a prediction. Using the pipeline will ensure that the transform is always performed correctly on input data.
First, we can define the model as a pipeline.
...
# define model to evaluate
model = SVC(gamma='scale', class_weight='balanced')
# power transform then fit model
pipeline = Pipeline(steps=[('t',PowerTransformer()), ('m',model)])
Once defined, we can fit it on the entire training dataset.
... # fit the model pipeline.fit(X, y)
Once fit, we can use it to make predictions for new data by calling the predict() function. This will return the class label of 0 for “no cancer”, or 1 for “cancer“.
For example:
... # define a row of data row = [...] # make prediction yhat = model.predict([row])
To demonstrate this, we can use the fit model to make some predictions of labels for a few cases where we know if the case is a no cancer or cancer.
The complete example is listed below.
# fit a model and make predictions for the on the mammography dataset
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import PowerTransformer
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
# load the dataset
def load_dataset(full_path):
# load the dataset as a numpy array
data = read_csv(full_path, header=None)
# retrieve numpy array
data = data.values
# split into input and output elements
X, y = data[:, :-1], data[:, -1]
# label encode the target variable to have the classes 0 and 1
y = LabelEncoder().fit_transform(y)
return X, y
# define the location of the dataset
full_path = 'mammography.csv'
# load the dataset
X, y = load_dataset(full_path)
# define model to evaluate
model = SVC(gamma='scale', class_weight='balanced')
# power transform then fit model
pipeline = Pipeline(steps=[('t',PowerTransformer()), ('m',model)])
# fit the model
pipeline.fit(X, y)
# evaluate on some no cancer cases (known class 0)
print('No Cancer:')
data = [[0.23001961,5.0725783,-0.27606055,0.83244412,-0.37786573,0.4803223],
[0.15549112,-0.16939038,0.67065219,-0.85955255,-0.37786573,-0.94572324],
[-0.78441482,-0.44365372,5.6747053,-0.85955255,-0.37786573,-0.94572324]]
for row in data:
# make prediction
yhat = pipeline.predict([row])
# get the label
label = yhat[0]
# summarize
print('>Predicted=%d (expected 0)' % (label))
# evaluate on some cancer (known class 1)
print('Cancer:')
data = [[2.0158239,0.15353258,-0.32114211,2.1923706,-0.37786573,0.96176503],
[2.3191888,0.72860087,-0.50146835,-0.85955255,-0.37786573,-0.94572324],
[0.19224721,-0.2003556,-0.230979,1.2003796,2.2620867,1.132403]]
for row in data:
# make prediction
yhat = pipeline.predict([row])
# get the label
label = yhat[0]
# summarize
print('>Predicted=%d (expected 1)' % (label))
Running the example first fits the model on the entire training dataset.
Then the fit model used to predict the label of no cancer cases is chosen from the dataset file. We can see that all cases are correctly predicted.
Then some cases of actual cancer are used as input to the model and the label is predicted. As we might have hoped, the correct labels are predicted for all cases.
No Cancer: >Predicted=0 (expected 0) >Predicted=0 (expected 0) >Predicted=0 (expected 0) Cancer: >Predicted=1 (expected 1) >Predicted=1 (expected 1) >Predicted=1 (expected 1)
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
- Comparative Evaluation Of Pattern Recognition Techniques For Detection Of Microcalcifications In Mammography, 1993.
- SMOTE: Synthetic Minority Over-sampling Technique, 2002.
APIs
- sklearn.model_selection.RepeatedStratifiedKFold API.
- sklearn.metrics.roc_auc_score API.
- sklearn.dummy.DummyClassifier API.
- sklearn.svm.SVC API.
Dataset
Summary
In this tutorial, you discovered how to develop and evaluate models for imbalanced mammography cancer classification dataset.
Specifically, you learned:
- How to load and explore the dataset and generate ideas for data preparation and model selection.
- How to evaluate a suite of machine learning models and improve their performance with data cost-sensitive techniques.
- How to fit a final model and use it to predict class labels for specific cases.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post Imbalanced Classification Model to Detect Mammography Microcalcifications appeared first on Machine Learning Mastery.
