How to Develop a Neural Net for Predicting Disturbances in the Ionosphere

Author: Jason Brownlee

It can be challenging to develop a neural network predictive model for a new dataset.

One approach is to first inspect the dataset and develop ideas for what models might work, then explore the learning dynamics of simple models on the dataset, then finally develop and tune a model for the dataset with a robust test harness.

This process can be used to develop effective neural network models for classification and regression predictive modeling problems.

In this tutorial, you will discover how to develop a Multilayer Perceptron neural network model for the ionosphere binary classification dataset.

After completing this tutorial, you will know:

How to load and summarize the ionosphere dataset and use the results to suggest data preparations and model configurations to use.
How to explore the learning dynamics of simple MLP models on the dataset.
How to develop robust estimates of model performance, tune model performance, and make predictions on new data.

Let’s get started.

How to Develop a Neural Net for Predicting Disturbances in the Ionosphere
Photo by Sergey Pesterev, some rights reserved.

Tutorial Overview

This tutorial is divided into four parts; they are:

Ionosphere Binary Classification Dataset
Neural Network Learning Dynamics
Evaluating and Tuning MLP Models
Final Model and Make Predictions

Ionosphere Binary Classification Dataset

The first step is to define and explore the dataset.

We will be working with the “Ionosphere” standard binary classification dataset.

This dataset involves predicting whether a structure is in the atmosphere or not given radar returns.

You can learn more about the dataset here:

You can see the first few rows of the dataset below.

1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300,g
1,0,1,-0.18829,0.93035,-0.36156,-0.10868,-0.93597,1,-0.04549,0.50874,-0.67743,0.34432,-0.69707,-0.51685,-0.97515,0.05499,-0.62237,0.33109,-1,-0.13151,-0.45300,-0.18056,-0.35734,-0.20332,-0.26569,-0.20468,-0.18401,-0.19040,-0.11593,-0.16626,-0.06288,-0.13738,-0.02447,b
1,0,1,-0.03365,1,0.00485,1,-0.12062,0.88965,0.01198,0.73082,0.05346,0.85443,0.00827,0.54591,0.00299,0.83775,-0.13644,0.75535,-0.08540,0.70887,-0.27502,0.43385,-0.12062,0.57528,-0.40220,0.58984,-0.22145,0.43100,-0.17365,0.60436,-0.24180,0.56045,-0.38238,g
1,0,1,-0.45161,1,1,0.71216,-1,0,0,0,0,0,0,-1,0.14516,0.54094,-0.39330,-1,-0.54467,-0.69975,1,0,0,1,0.90695,0.51613,1,1,-0.20099,0.25682,1,-0.32382,1,b
1,0,1,-0.02401,0.94140,0.06531,0.92106,-0.23255,0.77152,-0.16399,0.52798,-0.20275,0.56409,-0.00712,0.34395,-0.27457,0.52940,-0.21780,0.45107,-0.17813,0.05982,-0.35575,0.02309,-0.52879,0.03286,-0.65158,0.13290,-0.53206,0.02431,-0.62197,-0.05707,-0.59573,-0.04608,-0.65697,g
...

We can see that the values are all numeric and perhaps in the range [-1, 1]. This suggests some type of scaling would probably not be needed.

We can also see that the label is a string (“g” and “b“), suggesting that the values will need to be encoded to 0 and 1 prior to fitting a model.

We can load the dataset as a pandas DataFrame directly from the URL; for example:

# load the ionosphere dataset and summarize the shape
from pandas import read_csv
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
# load the dataset
df = read_csv(url, header=None)
# summarize shape
print(df.shape)

Running the example loads the dataset directly from the URL and reports the shape of the dataset.

In this case, we can see that the dataset has 35 variables (34 input and one output) and that the dataset has 351 rows of data.

This is not many rows of data for a neural network and suggests that a small network, perhaps with regularization, would be appropriate.

It also suggests that using k-fold cross-validation would be a good idea given that it will give a more reliable estimate of model performance than a train/test split and because a single model will fit in seconds instead of hours or days with the largest datasets.

(351, 35)

Next, we can learn more about the dataset by looking at summary statistics and a plot of the data.

# show summary statistics and plots of the ionosphere dataset
from pandas import read_csv
from matplotlib import pyplot
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
# load the dataset
df = read_csv(url, header=None)
# show summary statistics
print(df.describe())
# plot histograms
df.hist()
pyplot.show()

Running the example first loads the data before and then prints summary statistics for each variable.

We can see that the mean values for each variable are in the tens, with values ranging from -1 to 1. This confirms that scaling the data is probably not required.

0      1           2   ...          31          32          33
count  351.000000  351.0  351.000000  ...  351.000000  351.000000  351.000000
mean     0.891738    0.0    0.641342  ...   -0.003794    0.349364    0.014480
std      0.311155    0.0    0.497708  ...    0.513574    0.522663    0.468337
min      0.000000    0.0   -1.000000  ...   -1.000000   -1.000000   -1.000000
25%      1.000000    0.0    0.472135  ...   -0.242595    0.000000   -0.165350
50%      1.000000    0.0    0.871110  ...    0.000000    0.409560    0.000000
75%      1.000000    0.0    1.000000  ...    0.200120    0.813765    0.171660
max      1.000000    0.0    1.000000  ...    1.000000    1.000000    1.000000

A histogram plot is then created for each variable.

We can see that many variables have a Gaussian or Gaussian-like distribution.

We may have some benefit in using a power transform on each variable in order to make the probability distribution less skewed which will likely improve model performance.

Histograms of the Ionosphere Classification Dataset

Now that we are familiar with the dataset, let’s explore how we might develop a neural network model.

Neural Network Learning Dynamics

We will develop a Multilayer Perceptron (MLP) model for the dataset using TensorFlow.

We cannot know what model architecture of learning hyperparameters would be good or best for this dataset, so we must experiment and discover what works well.

Given that the dataset is small, a small batch size is probably a good idea, e.g. 16 or 32 rows. Using the Adam version of stochastic gradient descent is a good idea when getting started as it will automatically adapts the learning rate and works well on most datasets.

Before we evaluate models in earnest, it is a good idea to review the learning dynamics and tune the model architecture and learning configuration until we have stable learning dynamics, then look at getting the most out of the model.

We can do this by using a simple train/test split of the data and review plots of the learning curves. This will help us see if we are over-learning or under-learning; then we can adapt the configuration accordingly.

First, we must ensure all input variables are floating-point values and encode the target label as integer values 0 and 1.

...
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)

Next, we can split the dataset into input and output variables, then into 67/33 train and test sets.

...
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

We can define a minimal MLP model. In this case, we will use one hidden layer with 10 nodes and one output layer (chosen arbitrarily). We will use the ReLU activation function in the hidden layer and the “he_normal” weight initialization, as together, they are a good practice.

The output of the model is a sigmoid activation for binary classification and we will minimize binary cross-entropy loss.

...
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')

We will fit the model for 200 training epochs (chosen arbitrarily) with a batch size of 32 because it is a small dataset.

We are fitting the model on raw data, which we think might be a good idea, but it is an important starting point.

...
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=32, verbose=0, validation_data=(X_test,y_test))

At the end of training, we will evaluate the model’s performance on the test dataset and report performance as the classification accuracy.

...
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)

Finally, we will plot learning curves of the cross-entropy loss on the train and test sets during training.

...
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()

Tying this all together, the complete example of evaluating our first MLP on the ionosphere dataset is listed below.

# fit a simple mlp model on the ionosphere and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=32, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()

Running the example first fits the model on the training dataset, then reports the classification accuracy on the test dataset.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

In this case, we can see that the model achieved an accuracy of about 88 percent, which is a good baseline in performance that we might be able to improve upon.

Accuracy: 0.888

Line plots of the loss on the train and test sets are then created.

We can see that the model appears to converge but has overfit the training dataset.

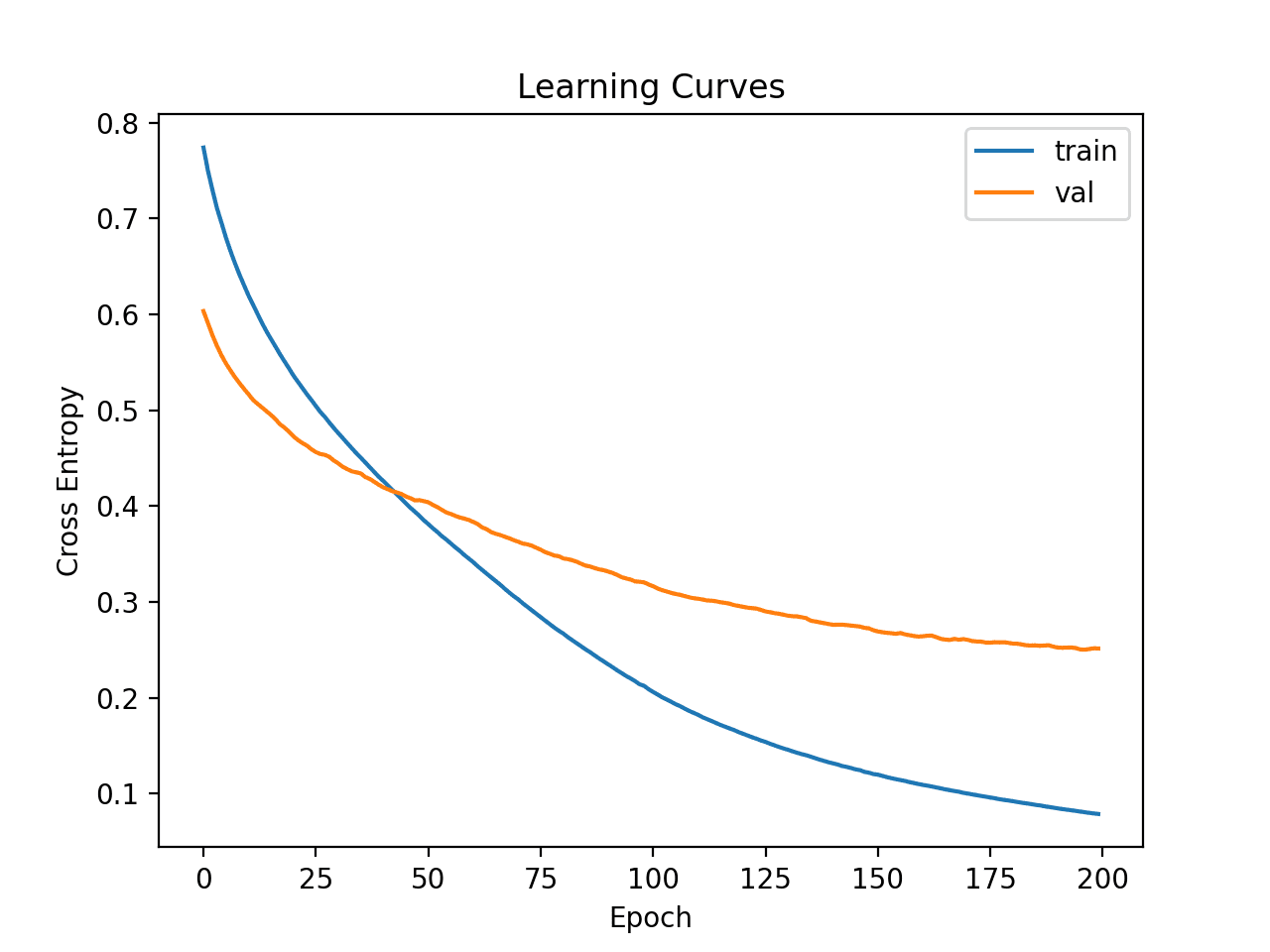
Learning Curves of Simple MLP on Ionosphere Dataset

Let’s try increasing the capacity of the model.

This will slow down learning for the same learning hyperparameters and may offer better accuracy.

We will add a second hidden layer with eight nodes, chosen arbitrarily.

...
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))

The complete example is listed below.

# fit a deeper mlp model on the ionosphere and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=32, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()

Running the example first fits the model on the training dataset, then reports the accuracy on the test dataset.

In this case, we can see a slight improvement in accuracy to about 93 percent, although the high variance of the train/test split means that this evaluation is not reliable.

Accuracy: 0.931

Learning curves for the loss on the train and test sets are then plotted. We can see that the model still appears to show an overfitting behavior.

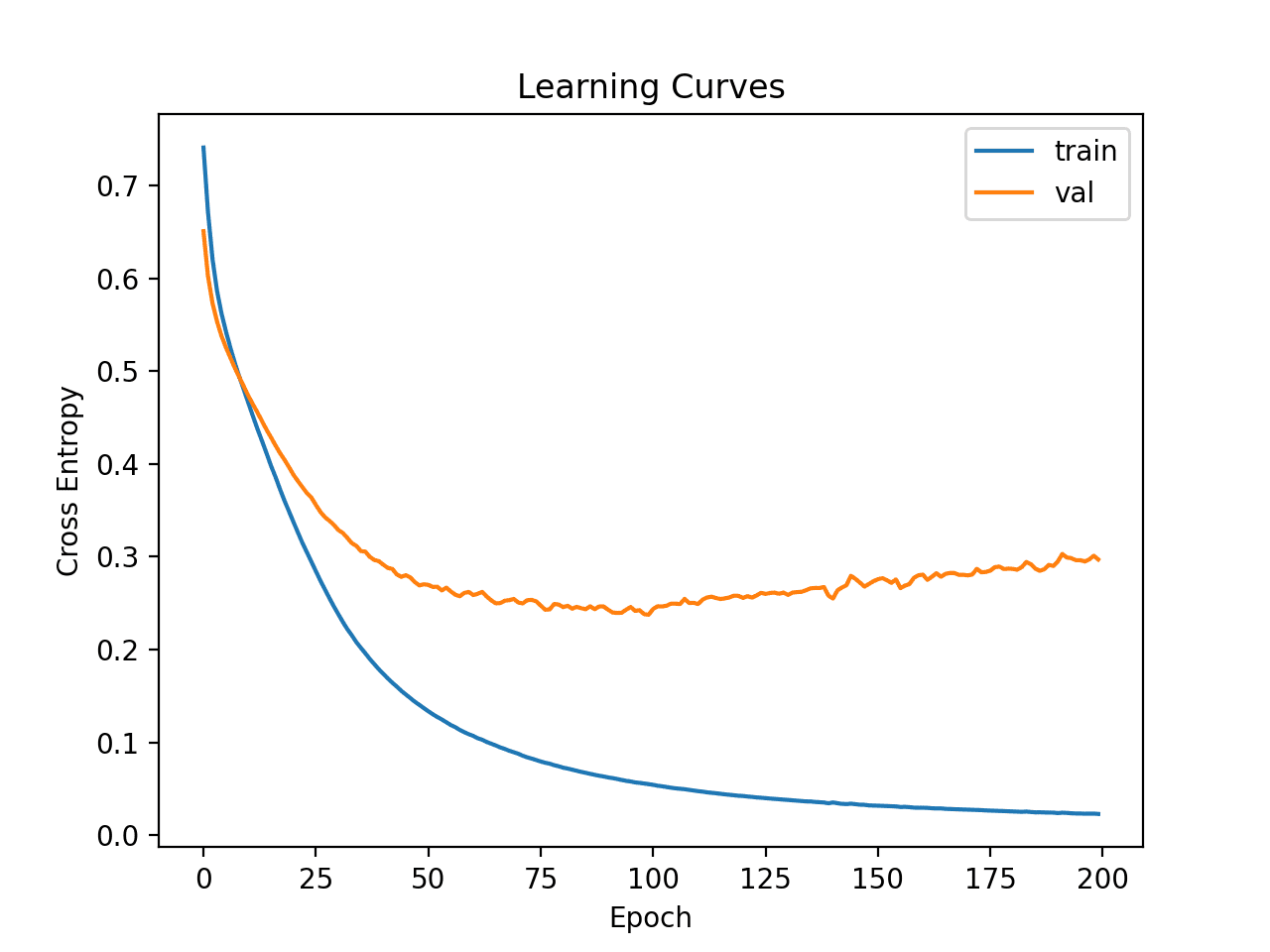
Learning Curves of Deeper MLP on the Ionosphere Dataset

Finally, we can try a wider network.

We will increase the number of nodes in the first hidden layer from 10 to 50, and in the second hidden layer from 8 to 10.

This will add more capacity to the model, slow down learning, and may further improve results.

...
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))

We will also reduce the number of training epochs from 200 to 100.

...
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0, validation_data=(X_test,y_test))

The complete example is listed below.

# fit a wider mlp model on the ionosphere and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()

Running the example first fits the model on the training dataset, then reports the accuracy on the test dataset.

In this case, the model achieves a better accuracy score, with a value of about 94 percent. We will ignore model performance for now.

Accuracy: 0.940

Line plots of the learning curves are created showing that the model achieved a reasonable fit and had more than enough time to converge.

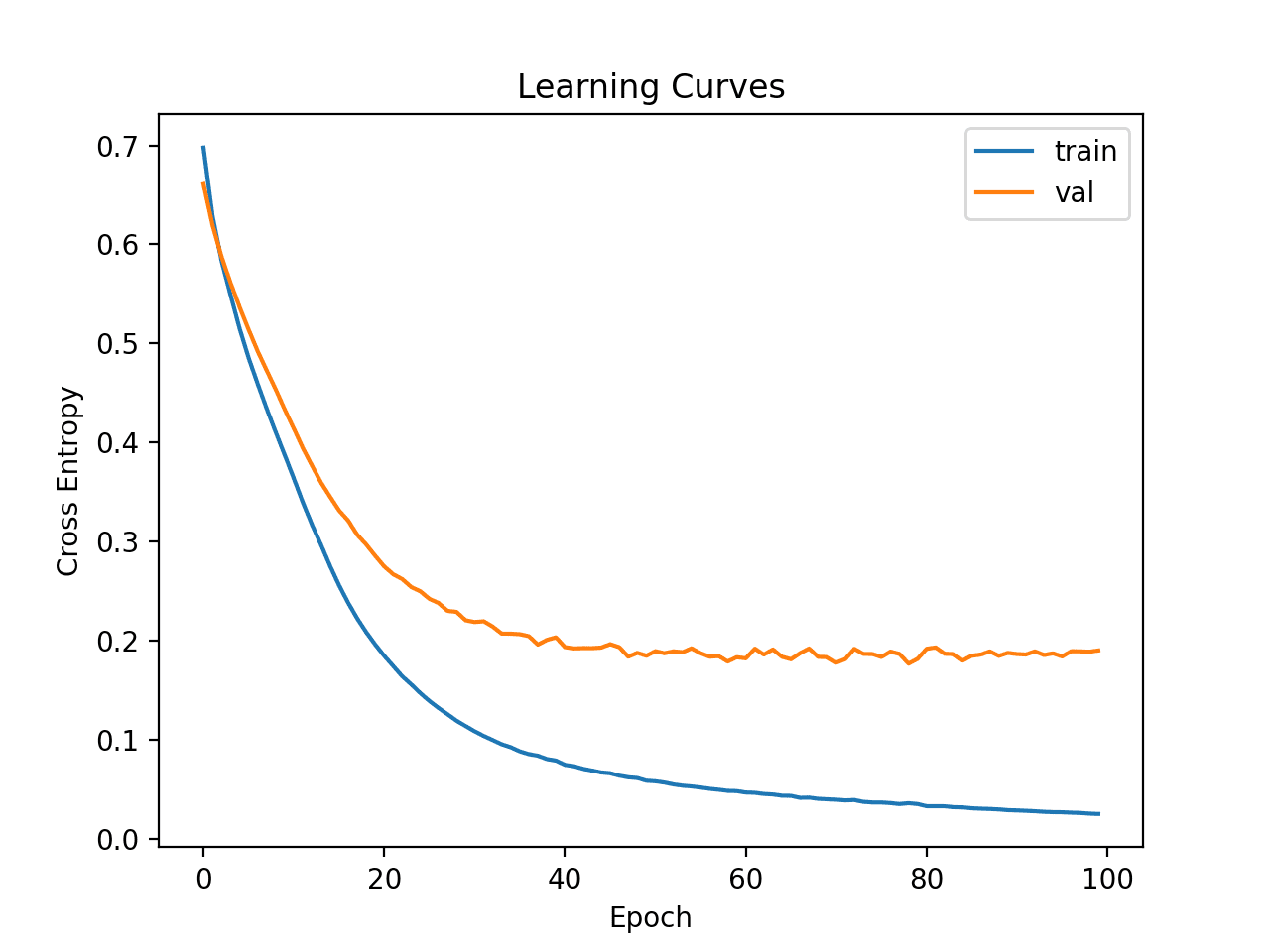
Learning Curves of Wider MLP on the Ionosphere Dataset

Now that we have some idea of the learning dynamics for simple MLP models on the dataset, we can look at evaluating the performance of the models as well as tuning the configuration of the models.

Evaluating and Tuning MLP Models

The k-fold cross-validation procedure can provide a more reliable estimate of MLP performance, although it can be very slow.

This is because k models must be fit and evaluated. This is not a problem when the dataset size is small, such as the ionosphere dataset.

We can use the StratifiedKFold class and enumerate each fold manually, fit the model, evaluate it, and then report the mean of the evaluation scores at the end of the procedure.

# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
	# fit and evaluate the model...
	...
...
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))

We can use this framework to develop a reliable estimate of MLP model performance with a range of different data preparations, model architectures, and learning configurations.

It is important that we first developed an understanding of the learning dynamics of the model on the dataset in the previous section before using k-fold cross-validation to estimate the performance. If we started to tune the model directly, we might get good results, but if not, we might have no idea of why, e.g. that the model was over or under fitting.

If we make large changes to the model again, it is a good idea to go back and confirm that the model is converging appropriately.

The complete example of this framework to evaluate the base MLP model from the previous section is listed below.

# k-fold cross-validation of base model for the ionosphere dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# prepare cross validation
kfold = StratifiedKFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
	# split data
	X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
	# determine the number of input features
	n_features = X.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
	model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
	model.add(Dense(1, activation='sigmoid'))
	# compile the model
	model.compile(optimizer='adam', loss='binary_crossentropy')
	# fit the model
	model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0)
	# predict test set
	yhat = model.predict_classes(X_test)
	# evaluate predictions
	score = accuracy_score(y_test, yhat)
	print('>%.3f' % score)
	scores.append(score)
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))

Running the example reports the model performance each iteration of the evaluation procedure and reports the mean and standard deviation of classification accuracy at the end of the run.

In this case, we can see that the MLP model achieved a mean accuracy of about 93.4 percent.

We will use this result as our baseline to see if we can achieve better performance.

>0.972
>0.886
>0.943
>0.886
>0.914
>0.943
>0.943
>1.000
>0.971
>0.886
Mean Accuracy: 0.934 (0.039)

Next, let’s try adding regularization to reduce overfitting of the model.

In this case, we can add dropout layers between the hidden layers of the network. For example:

...
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))

The complete example of the MLP model with dropout is listed below.

# k-fold cross-validation of the MLP with dropout for the ionosphere dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Dropout
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# prepare cross validation
kfold = StratifiedKFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
	# split data
	X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
	# determine the number of input features
	n_features = X.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
	model.add(Dropout(0.4))
	model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
	model.add(Dropout(0.4))
	model.add(Dense(1, activation='sigmoid'))
	# compile the model
	model.compile(optimizer='adam', loss='binary_crossentropy')
	# fit the model
	model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0)
	# predict test set
	yhat = model.predict_classes(X_test)
	# evaluate predictions
	score = accuracy_score(y_test, yhat)
	print('>%.3f' % score)
	scores.append(score)
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))

Running reports the mean and standard deviation of the classification accuracy at the end of the run.

In this case, we can see that the MLP model with dropout achieves better results with an accuracy of about 94.6 percent compared to 93.4 percent without dropout

Mean Accuracy: 0.946 (0.043)

Finally, we will try reducing the batch size from 32 down to 8.

This will result in more noisy gradients and may also slow down the speed at which the model is learning the problem.

...
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0)

The complete example is listed below.

# k-fold cross-validation of the MLP with dropout for the ionosphere dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Dropout
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# prepare cross validation
kfold = StratifiedKFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
	# split data
	X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
	# determine the number of input features
	n_features = X.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
	model.add(Dropout(0.4))
	model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
	model.add(Dropout(0.4))
	model.add(Dense(1, activation='sigmoid'))
	# compile the model
	model.compile(optimizer='adam', loss='binary_crossentropy')
	# fit the model
	model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0)
	# predict test set
	yhat = model.predict_classes(X_test)
	# evaluate predictions
	score = accuracy_score(y_test, yhat)
	print('>%.3f' % score)
	scores.append(score)
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))

Running reports the mean and standard deviation of the classification accuracy at the end of the run.

In this case, we can see that the MLP model with dropout achieves slightly better results with an accuracy of about 94.9 percent.

Mean Accuracy: 0.949 (0.042)

We will use this configuration as our final model.

We could continue to test alternate configurations to the model architecture (more or fewer nodes or layers), learning hyperparameters (more or fewer batches), and data transforms.

I leave this as an exercise; let me know what you discover. Can you get better results?
Post your results in the comments below, I’d love to see what you get.

Next, let’s look at how we might fit a final model and use it to make predictions.

Final Model and Make Predictions

Once we choose a model configuration, we can train a final model on all available data and use it to make predictions on new data.

In this case, we will use the model with dropout and a small batch size as our final model.

We can prepare the data and fit the model as before, although on the entire dataset instead of a training subset of the dataset.

...
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
le = LabelEncoder()
y = le.fit_transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')

We can then use this model to make predictions on new data.

First, we can define a row of new data.

...
# define a row of new data
row = [1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300]

Note: I took this row from the first row of the dataset and the expected label is a ‘g‘.

We can then make a prediction.

...
# make prediction
yhat = model.predict_classes([row])

Then invert the transform on the prediction, so we can use or interpret the result in the correct label.

...
# invert transform to get label for class
yhat = le.inverse_transform(yhat)

And in this case, we will simply report the prediction.

...
# report prediction
print('Predicted: %s' % (yhat[0]))

Tying this all together, the complete example of fitting a final model for the ionosphere dataset and using it to make a prediction on new data is listed below.

# fit a final model and make predictions on new data for the ionosphere dataset
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Dropout
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
le = LabelEncoder()
y = le.fit_transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
model.fit(X, y, epochs=100, batch_size=8, verbose=0)
# define a row of new data
row = [1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300]
# make prediction
yhat = model.predict_classes([row])
# invert transform to get label for class
yhat = le.inverse_transform(yhat)
# report prediction
print('Predicted: %s' % (yhat[0]))

Running the example fits the model on the entire dataset and makes a prediction for a single row of new data.

In this case, we can see that the model predicted a “g” label for the input row.

Predicted: g

Summary

In this tutorial, you discovered how to develop a Multilayer Perceptron neural network model for the ionosphere binary classification dataset.

Specifically, you learned:

How to load and summarize the ionosphere dataset and use the results to suggest data preparations and model configurations to use.
How to explore the learning dynamics of simple MLP models on the dataset.
How to develop robust estimates of model performance, tune model performance and make predictions on new data.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

The post How to Develop a Neural Net for Predicting Disturbances in the Ionosphere appeared first on Machine Learning Mastery.

Go to Source

How to Develop a Neural Net for Predicting Disturbances in the Ionosphere

Tutorial Overview

Ionosphere Binary Classification Dataset

Neural Network Learning Dynamics

Evaluating and Tuning MLP Models

Final Model and Make Predictions

Further Reading

Tutorials

Summary