Author: Jason Brownlee
Iterated Local Search is a stochastic global optimization algorithm.
It involves the repeated application of a local search algorithm to modified versions of a good solution found previously. In this way, it is like a clever version of the stochastic hill climbing with random restarts algorithm.
The intuition behind the algorithm is that random restarts can help to locate many local optima in a problem and that better local optima are often close to other local optima. Therefore modest perturbations to existing local optima may locate better or even best solutions to an optimization problem.
In this tutorial, you will discover how to implement the iterated local search algorithm from scratch.
After completing this tutorial, you will know:
- Iterated local search is a stochastic global search optimization algorithm that is a smarter version of stochastic hill climbing with random restarts.
- How to implement stochastic hill climbing with random restarts from scratch.
- How to implement and apply the iterated local search algorithm to a nonlinear objective function.
Let’s get started.

Iterated Local Search From Scratch in Python
Photo by Susanne Nilsson, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
- What Is Iterated Local Search
- Ackley Objective Function
- Stochastic Hill Climbing Algorithm
- Stochastic Hill Climbing With Random Restarts
- Iterated Local Search Algorithm
What Is Iterated Local Search
Iterated Local Search, or ILS for short, is a stochastic global search optimization algorithm.
It is related to or an extension of stochastic hill climbing and stochastic hill climbing with random starts.
It’s essentially a more clever version of Hill-Climbing with Random Restarts.
— Page 26, Essentials of Metaheuristics, 2011.
Stochastic hill climbing is a local search algorithm that involves making random modifications to an existing solution and accepting the modification only if it results in better results than the current working solution.
Local search algorithms in general can get stuck in local optima. One approach to address this problem is to restart the search from a new randomly selected starting point. The restart procedure can be performed many times and may be triggered after a fixed number of function evaluations or if no further improvement is seen for a given number of algorithm iterations. This algorithm is called stochastic hill climbing with random restarts.
The simplest possibility to improve upon a cost found by LocalSearch is to repeat the search from another starting point.
— Page 132, Handbook of Metaheuristics, 3rd edition 2019.
Iterated local search is similar to stochastic hill climbing with random restarts, except rather than selecting a random starting point for each restart, a point is selected based on a modified version of the best point found so far during the broader search.
The perturbation of the best solution so far is like a large jump in the search space to a new region, whereas the perturbations made by the stochastic hill climbing algorithm are much smaller, confined to a specific region of the search space.
The heuristic here is that you can often find better local optima near to the one you’re presently in, and walking from local optimum to local optimum in this way often outperforms just trying new locations entirely at random.
— Page 26, Essentials of Metaheuristics, 2011.
This allows the search to be performed at two levels. The hill climbing algorithm is the local search for getting the most out of a specific candidate solution or region of the search space, and the restart approach allows different regions of the search space to be explored.
In this way, the algorithm Iterated Local Search explores multiple local optima in the search space, increasing the likelihood of locating the global optima.
The Iterated Local Search was proposed for combinatorial optimization problems, such as the traveling salesman problem (TSP), although it can be applied to continuous function optimization by using different step sizes in the search space: smaller steps for the hill climbing and larger steps for the random restart.
Now that we are familiar with the Iterated Local Search algorithm, let’s explore how to implement the algorithm from scratch.
Ackley Objective Function
First, let’s define a channeling optimization problem as the basis for implementing the Iterated Local Search algorithm.
The Ackley function is an example of a multimodal objective function that has a single global optima and multiple local optima in which a local search might get stuck.
As such, a global optimization technique is required. It is a two-dimensional objective function that has a global optima at [0,0], which evaluates to 0.0.
The example below implements the Ackley and creates a three-dimensional surface plot showing the global optima and multiple local optima.
# ackley multimodal function from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # define range for input r_min, r_max = -5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()
Running the example creates the surface plot of the Ackley function showing the vast number of local optima.
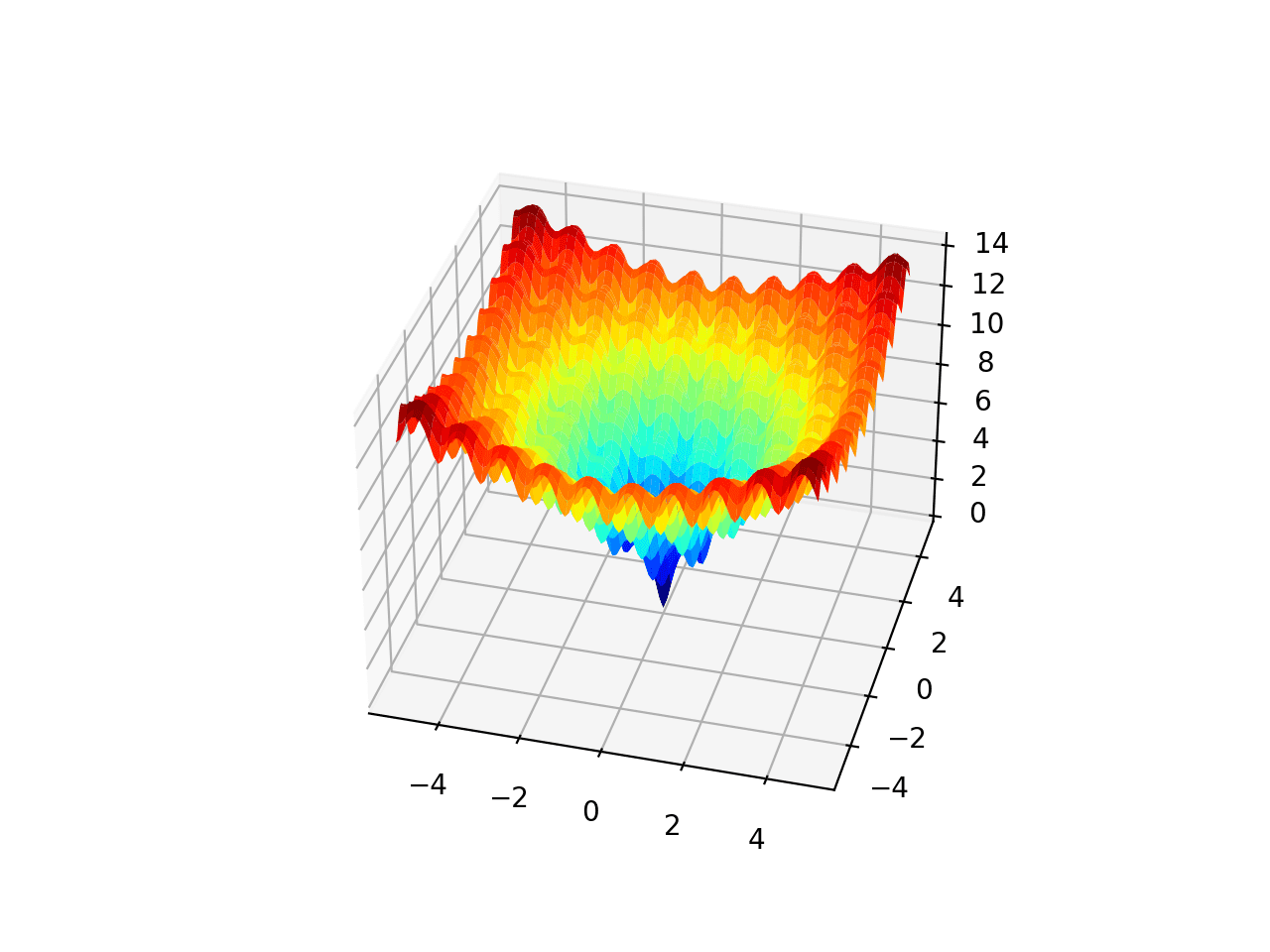
3D Surface Plot of the Ackley Multimodal Function
We will use this as the basis for implementing and comparing a simple stochastic hill climbing algorithm, stochastic hill climbing with random restarts, and finally iterated local search.
We would expect a stochastic hill climbing algorithm to get stuck easily in local minima. We would expect stochastic hill climbing with restarts to find many local minima, and we would expect iterated local search to perform better than either method on this problem if configured appropriately.
Stochastic Hill Climbing Algorithm
Core to the Iterated Local Search algorithm is a local search, and in this tutorial, we will use the Stochastic Hill Climbing algorithm for this purpose.
The Stochastic Hill Climbing algorithm involves first generating a random starting point and current working solution, then generating perturbed versions of the current working solution and accepting them if they are better than the current working solution.
Given that we are working on a continuous optimization problem, a solution is a vector of values to be evaluated by the objective function, in this case, a point in a two-dimensional space bounded by -5 and 5.
We can generate a random point by sampling the search space with a uniform probability distribution. For example:
... # generate a random point in the search space solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
We can generate perturbed versions of a currently working solution using a Gaussian probability distribution with the mean of the current values in the solution and a standard deviation controlled by a hyperparameter that controls how far the search is allowed to explore from the current working solution.
We will refer to this hyperparameter as “step_size“, for example:
... # generate a perturbed version of a current working solution candidate = solution + randn(len(bounds)) * step_size
Importantly, we must check that generated solutions are within the search space.
This can be achieved with a custom function named in_bounds() that takes a candidate solution and the bounds of the search space and returns True if the point is in the search space, False otherwise.
# check if a point is within the bounds of the search def in_bounds(point, bounds): # enumerate all dimensions of the point for d in range(len(bounds)): # check if out of bounds for this dimension if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]: return False return True
This function can then be called during the hill climb to confirm that new points are in the bounds of the search space, and if not, new points can be generated.
Tying this together, the function hillclimbing() below implements the stochastic hill climbing local search algorithm. It takes the name of the objective function, bounds of the problem, number of iterations, and steps size as arguments and returns the best solution and its evaluation.
# hill climbing local search algorithm
def hillclimbing(objective, bounds, n_iterations, step_size):
# generate an initial point
solution = None
while solution is None or not in_bounds(solution, bounds):
solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
# evaluate the initial point
solution_eval = objective(solution)
# run the hill climb
for i in range(n_iterations):
# take a step
candidate = None
while candidate is None or not in_bounds(candidate, bounds):
candidate = solution + randn(len(bounds)) * step_size
# evaluate candidate point
candidte_eval = objective(candidate)
# check if we should keep the new point
if candidte_eval <= solution_eval:
# store the new point
solution, solution_eval = candidate, candidte_eval
# report progress
print('>%d f(%s) = %.5f' % (i, solution, solution_eval))
return [solution, solution_eval]
We can test this algorithm on the Ackley function.
We will fix the seed for the pseudorandom number generator to ensure we get the same results each time the code is run.
The algorithm will be run for 1,000 iterations and a step size of 0.05 units will be used; both hyperparameters were chosen after a little trial and error.
At the end of the run, we will report the best solution found.
...
# seed the pseudorandom number generator
seed(1)
# define range for input
bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]])
# define the total iterations
n_iterations = 1000
# define the maximum step size
step_size = 0.05
# perform the hill climbing search
best, score = hillclimbing(objective, bounds, n_iterations, step_size)
print('Done!')
print('f(%s) = %f' % (best, score))
Tying this together, the complete example of applying the stochastic hill climbing algorithm to the Ackley objective function is listed below.
# hill climbing search of the ackley objective function
from numpy import asarray
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
from numpy.random import randn
from numpy.random import rand
from numpy.random import seed
# objective function
def objective(v):
x, y = v
return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
# check if a point is within the bounds of the search
def in_bounds(point, bounds):
# enumerate all dimensions of the point
for d in range(len(bounds)):
# check if out of bounds for this dimension
if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]:
return False
return True
# hill climbing local search algorithm
def hillclimbing(objective, bounds, n_iterations, step_size):
# generate an initial point
solution = None
while solution is None or not in_bounds(solution, bounds):
solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
# evaluate the initial point
solution_eval = objective(solution)
# run the hill climb
for i in range(n_iterations):
# take a step
candidate = None
while candidate is None or not in_bounds(candidate, bounds):
candidate = solution + randn(len(bounds)) * step_size
# evaluate candidate point
candidte_eval = objective(candidate)
# check if we should keep the new point
if candidte_eval <= solution_eval:
# store the new point
solution, solution_eval = candidate, candidte_eval
# report progress
print('>%d f(%s) = %.5f' % (i, solution, solution_eval))
return [solution, solution_eval]
# seed the pseudorandom number generator
seed(1)
# define range for input
bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]])
# define the total iterations
n_iterations = 1000
# define the maximum step size
step_size = 0.05
# perform the hill climbing search
best, score = hillclimbing(objective, bounds, n_iterations, step_size)
print('Done!')
print('f(%s) = %f' % (best, score))
Running the example performs the stochastic hill climbing search on the objective function. Each improvement found during the search is reported and the best solution is then reported at the end of the search.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see about 13 improvements during the search and a final solution of about f(-0.981, 1.965), resulting in an evaluation of about 5.381, which is far from f(0.0, 0.0) = 0.
>0 f([-0.85618854 2.1495965 ]) = 6.46986 >1 f([-0.81291816 2.03451957]) = 6.07149 >5 f([-0.82903902 2.01531685]) = 5.93526 >7 f([-0.83766043 1.97142393]) = 5.82047 >9 f([-0.89269139 2.02866012]) = 5.68283 >12 f([-0.8988359 1.98187164]) = 5.55899 >13 f([-0.9122303 2.00838942]) = 5.55566 >14 f([-0.94681334 1.98855174]) = 5.43024 >15 f([-0.98117198 1.94629146]) = 5.39010 >23 f([-0.97516403 1.97715161]) = 5.38735 >39 f([-0.98628044 1.96711371]) = 5.38241 >362 f([-0.9808789 1.96858459]) = 5.38233 >629 f([-0.98102417 1.96555308]) = 5.38194 Done! f([-0.98102417 1.96555308]) = 5.381939
Next, we will modify the algorithm to perform random restarts and see if we can achieve better results.
Stochastic Hill Climbing With Random Restarts
The Stochastic Hill Climbing With Random Restarts algorithm involves the repeated running of the Stochastic Hill Climbing algorithm and keeping track of the best solution found.
First, let’s modify the hillclimbing() function to take the starting point of the search rather than generating it randomly. This will help later when we implement the Iterated Local Search algorithm later.
# hill climbing local search algorithm def hillclimbing(objective, bounds, n_iterations, step_size, start_pt): # store the initial point solution = start_pt # evaluate the initial point solution_eval = objective(solution) # run the hill climb for i in range(n_iterations): # take a step candidate = None while candidate is None or not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # evaluate candidate point candidte_eval = objective(candidate) # check if we should keep the new point if candidte_eval <= solution_eval: # store the new point solution, solution_eval = candidate, candidte_eval return [solution, solution_eval]
Next, we can implement the random restart algorithm by repeatedly calling the hillclimbing() function a fixed number of times.
Each call, we will generate a new randomly selected starting point for the hill climbing search.
... # generate a random initial point for the search start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # perform a stochastic hill climbing search solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt)
We can then inspect the result and keep it if it is better than any result of the search we have seen so far.
...
# check for new best
if solution_eval < best_eval:
best, best_eval = solution, solution_eval
print('Restart %d, best: f(%s) = %.5f' % (n, best, best_eval))
Tying this together, the random_restarts() function implemented the stochastic hill climbing algorithm with random restarts.
# hill climbing with random restarts algorithm
def random_restarts(objective, bounds, n_iter, step_size, n_restarts):
best, best_eval = None, 1e+10
# enumerate restarts
for n in range(n_restarts):
# generate a random initial point for the search
start_pt = None
while start_pt is None or not in_bounds(start_pt, bounds):
start_pt = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
# perform a stochastic hill climbing search
solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt)
# check for new best
if solution_eval < best_eval:
best, best_eval = solution, solution_eval
print('Restart %d, best: f(%s) = %.5f' % (n, best, best_eval))
return [best, best_eval]
We can then apply this algorithm to the Ackley objective function. In this case, we will limit the number of random restarts to 30, chosen arbitrarily.
The complete example is listed below.
# hill climbing search with random restarts of the ackley objective function
from numpy import asarray
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
from numpy.random import randn
from numpy.random import rand
from numpy.random import seed
# objective function
def objective(v):
x, y = v
return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
# check if a point is within the bounds of the search
def in_bounds(point, bounds):
# enumerate all dimensions of the point
for d in range(len(bounds)):
# check if out of bounds for this dimension
if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]:
return False
return True
# hill climbing local search algorithm
def hillclimbing(objective, bounds, n_iterations, step_size, start_pt):
# store the initial point
solution = start_pt
# evaluate the initial point
solution_eval = objective(solution)
# run the hill climb
for i in range(n_iterations):
# take a step
candidate = None
while candidate is None or not in_bounds(candidate, bounds):
candidate = solution + randn(len(bounds)) * step_size
# evaluate candidate point
candidte_eval = objective(candidate)
# check if we should keep the new point
if candidte_eval <= solution_eval:
# store the new point
solution, solution_eval = candidate, candidte_eval
return [solution, solution_eval]
# hill climbing with random restarts algorithm
def random_restarts(objective, bounds, n_iter, step_size, n_restarts):
best, best_eval = None, 1e+10
# enumerate restarts
for n in range(n_restarts):
# generate a random initial point for the search
start_pt = None
while start_pt is None or not in_bounds(start_pt, bounds):
start_pt = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
# perform a stochastic hill climbing search
solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt)
# check for new best
if solution_eval < best_eval:
best, best_eval = solution, solution_eval
print('Restart %d, best: f(%s) = %.5f' % (n, best, best_eval))
return [best, best_eval]
# seed the pseudorandom number generator
seed(1)
# define range for input
bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]])
# define the total iterations
n_iter = 1000
# define the maximum step size
step_size = 0.05
# total number of random restarts
n_restarts = 30
# perform the hill climbing search
best, score = random_restarts(objective, bounds, n_iter, step_size, n_restarts)
print('Done!')
print('f(%s) = %f' % (best, score))
Running the example will perform a stochastic hill climbing with random restarts search for the Ackley objective function. Each time an improved overall solution is discovered, it is reported and the final best solution found by the search is summarized.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see three improvements during the search and that the best solution found was approximately f(0.002, 0.002), which evaluated to about 0.009, which is much better than a single run of the hill climbing algorithm.
Restart 0, best: f([-0.98102417 1.96555308]) = 5.38194 Restart 2, best: f([1.96522236 0.98120013]) = 5.38191 Restart 4, best: f([0.00223194 0.00258853]) = 0.00998 Done! f([0.00223194 0.00258853]) = 0.009978
Next, let’s look at how we can implement the iterated local search algorithm.
Iterated Local Search Algorithm
The Iterated Local Search algorithm is a modified version of the stochastic hill climbing with random restarts algorithm.
The important difference is that the starting point for each application of the stochastic hill climbing algorithm is a perturbed version of the best point found so far.
We can implement this algorithm by using the random_restarts() function as a starting point. Each restart iteration, we can generate a modified version of the best solution found so far instead of a random starting point.
This can be achieved by using a step size hyperparameter, much like is used in the stochastic hill climber. In this case, a larger step size value will be used given the need for larger perturbations in the search space.
... # generate an initial point as a perturbed version of the last best start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size
Tying this together, the iterated_local_search() function is defined below.
# iterated local search algorithm
def iterated_local_search(objective, bounds, n_iter, step_size, n_restarts, p_size):
# define starting point
best = None
while best is None or not in_bounds(best, bounds):
best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
# evaluate current best point
best_eval = objective(best)
# enumerate restarts
for n in range(n_restarts):
# generate an initial point as a perturbed version of the last best
start_pt = None
while start_pt is None or not in_bounds(start_pt, bounds):
start_pt = best + randn(len(bounds)) * p_size
# perform a stochastic hill climbing search
solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt)
# check for new best
if solution_eval < best_eval:
best, best_eval = solution, solution_eval
print('Restart %d, best: f(%s) = %.5f' % (n, best, best_eval))
return [best, best_eval]
We can then apply the algorithm to the Ackley objective function. In this case, we will use a larger step size value of 1.0 for the random restarts, chosen after a little trial and error.
The complete example is listed below.
# iterated local search of the ackley objective function
from numpy import asarray
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
from numpy.random import randn
from numpy.random import rand
from numpy.random import seed
# objective function
def objective(v):
x, y = v
return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
# check if a point is within the bounds of the search
def in_bounds(point, bounds):
# enumerate all dimensions of the point
for d in range(len(bounds)):
# check if out of bounds for this dimension
if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]:
return False
return True
# hill climbing local search algorithm
def hillclimbing(objective, bounds, n_iterations, step_size, start_pt):
# store the initial point
solution = start_pt
# evaluate the initial point
solution_eval = objective(solution)
# run the hill climb
for i in range(n_iterations):
# take a step
candidate = None
while candidate is None or not in_bounds(candidate, bounds):
candidate = solution + randn(len(bounds)) * step_size
# evaluate candidate point
candidte_eval = objective(candidate)
# check if we should keep the new point
if candidte_eval <= solution_eval:
# store the new point
solution, solution_eval = candidate, candidte_eval
return [solution, solution_eval]
# iterated local search algorithm
def iterated_local_search(objective, bounds, n_iter, step_size, n_restarts, p_size):
# define starting point
best = None
while best is None or not in_bounds(best, bounds):
best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0])
# evaluate current best point
best_eval = objective(best)
# enumerate restarts
for n in range(n_restarts):
# generate an initial point as a perturbed version of the last best
start_pt = None
while start_pt is None or not in_bounds(start_pt, bounds):
start_pt = best + randn(len(bounds)) * p_size
# perform a stochastic hill climbing search
solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt)
# check for new best
if solution_eval < best_eval:
best, best_eval = solution, solution_eval
print('Restart %d, best: f(%s) = %.5f' % (n, best, best_eval))
return [best, best_eval]
# seed the pseudorandom number generator
seed(1)
# define range for input
bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]])
# define the total iterations
n_iter = 1000
# define the maximum step size
s_size = 0.05
# total number of random restarts
n_restarts = 30
# perturbation step size
p_size = 1.0
# perform the hill climbing search
best, score = iterated_local_search(objective, bounds, n_iter, s_size, n_restarts, p_size)
print('Done!')
print('f(%s) = %f' % (best, score))
Running the example will perform an Iterated Local Search of the Ackley objective function.
Each time an improved overall solution is discovered, it is reported and the final best solution found by the search is summarized at the end of the run.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see four improvements during the search and that the best solution found was two very small inputs that are close to zero, which evaluated to about 0.0003, which is better than either a single run of the hill climber or the hill climber with restarts.
Restart 0, best: f([-0.96775653 0.96853129]) = 3.57447 Restart 3, best: f([-4.50618519e-04 9.51020713e-01]) = 2.57996 Restart 5, best: f([ 0.00137423 -0.00047059]) = 0.00416 Restart 22, best: f([ 1.16431936e-04 -3.31358206e-06]) = 0.00033 Done! f([ 1.16431936e-04 -3.31358206e-06]) = 0.000330
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
- Essentials of Metaheuristics, 2011.
- Handbook of Metaheuristics, 3rd edition 2019.
Articles
Summary
In this tutorial, you discovered how to implement the iterated local search algorithm from scratch.
Specifically, you learned:
- Iterated local search is a stochastic global search optimization algorithm that is a smarter version of stochastic hill climbing with random restarts.
- How to implement stochastic hill climbing with random restarts from scratch.
- How to implement and apply the iterated local search algorithm to a nonlinear objective function.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post Iterated Local Search From Scratch in Python appeared first on Machine Learning Mastery.
