How to Develop a Random Subspace Ensemble With Python

Author: Jason Brownlee

Random Subspace Ensemble is a machine learning algorithm that combines the predictions from multiple decision trees trained on different subsets of columns in the training dataset.

Randomly varying the columns used to train each contributing member of the ensemble has the effect of introducing diversity into the ensemble and, in turn, can lift performance over using a single decision tree.

It is related to other ensembles of decision trees such as bootstrap aggregation (bagging) that creates trees using different samples of rows from the training dataset, and random forest that combines ideas from bagging and the random subspace ensemble.

Although decision trees are often used, the general random subspace method can be used with any machine learning model whose performance varies meaningfully with the choice of input features.

In this tutorial, you will discover how to develop random subspace ensembles for classification and regression.

After completing this tutorial, you will know:

Random subspace ensembles are created from decision trees fit on different samples of features (columns) in the training dataset.
How to use the random subspace ensemble for classification and regression with scikit-learn.
How to explore the effect of random subspace model hyperparameters on model performance.

Let’s get started.

How to Develop a Random Subspace Ensemble With Python
Photo by Marsel Minga, some rights reserved.

Tutorial Overview

This tutorial is divided into three parts; they are:

Random Subspace Ensemble
Random Subspace Ensemble via Bagging
1. Random Subspace Ensemble for Classification
2. Random Subspace Ensemble for Regression
Random Subspace Ensemble Hyperparameters
1. Explore Number of Trees
2. Explore Number of Features
3. Explore Alternate Algorithm

Random Subspace Ensemble

A predictive modeling problem consists of one or more input variables and a target variable.

A variable is a column in the data and is also often referred to as a feature. We can consider all input features together as defining an n-dimensional vector space, where n is the number of input features and each example (input row of data) is a point in the feature space.

This is a common conceptualization in machine learning and as input feature spaces become larger, the distance between points in the space increases, known generally as the curse of dimensionality.

A subset of input features can, therefore, be thought of as a subset of the input feature space, or a subspace.

Selecting features is a way of defining a subspace of the input feature space. For example, feature selection refers to an attempt to reduce the number of dimensions of the input feature space by selecting a subset of features to keep or a subset of features to delete, often based on their relationship to the target variable.

Alternatively, we can select random subsets of input features to define random subspaces. This can be used as the basis for an ensemble learning algorithm, where a model can be fit on each random subspace of features. This is referred to as a random subspace ensemble or the random subspace method.

The training data is usually described by a set of features. Different subsets of features, or called subspaces, provide different views on the data. Therefore, individual learners trained from different subspaces are usually diverse.

— Page 116, Ensemble Methods, 2012.

It was proposed by Tin Kam Ho in the 1998 paper titled “The Random Subspace Method For Constructing Decision Forests” where a decision tree is fit on each random subspace.

More generally, it is a diversity technique for ensemble learning that belongs to a class of methods that change the training dataset for each model in the attempt to reduce the correlation between the predictions of the models in the ensemble.

The procedure is as simple as selecting a random subset of input features (columns) for each model in the ensemble and fitting the model on the model in the entire training dataset. It can be augmented with additional changes, such as using a bootstrap or random sample of the rows in training dataset.

The classifier consists of multiple trees constructed systematically by pseudorandomly selecting subsets of components of the feature vector, that is, trees constructed in randomly chosen subspaces.

— The Random Subspace Method For Constructing Decision Forests, 1998.

As such, the random subspace ensemble is related to bootstrap aggregation (bagging) that introduces diversity by training each model, often a decision tree, on a different random sample of the training dataset, with replacement (e.g. the bootstrap sampling method). The random forest ensemble may also be considered a hybrid of both the bagging and random subset ensemble methods.

Algorithms that use different feature subsets are commonly referred to as random subspace methods …

— Page 21, Ensemble Machine Learning, 2012.

The random subspace method can be used with any machine learning algorithm, although it is well suited to models that are sensitive to large changes to the input features, such as decision trees and k-nearest neighbors.

It is appropriate for datasets that have a large number of input features, as it can result in good performance with good efficiency. If the dataset contains many irrelevant input features, it may be better to use feature selection as a data preparation technique as the prevalence of irrelevant features in subspaces may hurt the performance of the ensemble.

For data with a lot of redundant features, training a learner in a subspace will be not only effective but also efficient.

— Page 116, Ensemble Methods, 2012.

Now that we are familiar with the random subspace ensemble, let’s explore how we can implement the approach.

Random Subspace Ensemble via Bagging

We can implement the random subspace ensemble using bagging in scikit-learn.

Bagging is provided via the BaggingRegressor and BaggingClassifier classes.

We can configure bagging to be a random subspace ensemble by setting the “bootstrap” argument to “False” to turn off sampling of the training dataset rows and setting the maximum number of features to a given value via the “max_features” argument.

The default model for bagging is a decision tree, but it can be changed to any model we like.

We can demonstrate using bagging to implement a random subspace ensemble with decision trees for classification and regression.

Random Subspace Ensemble for Classification

In this section, we will look at developing a random subspace ensemble using bagging for a classification problem.

First, we can use the make_classification() function to create a synthetic binary classification problem with 1,000 examples and 20 input features.

The complete example is listed below.

# test classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# summarize the dataset
print(X.shape, y.shape)

Running the example creates the dataset and summarizes the shape of the input and output components.

(1000, 20) (1000,)

Next, we can configure a bagging model to be a random subspace ensemble for decision trees on this dataset.

Each model will be fit on a random subspace of 10 input features, chosen arbitrarily.

...
# define the random subspace ensemble model
model = BaggingClassifier(bootstrap=False, max_features=10)

We will evaluate the model using repeated stratified k-fold cross-validation, with three repeats and 10 folds. We will report the mean and standard deviation of the accuracy of the model across all repeats and folds.

# evaluate random subspace ensemble via bagging for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the random subspace ensemble model
model = BaggingClassifier(bootstrap=False, max_features=10)
# define the evaluation method
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model on the dataset
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report performance
print('Mean Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

Running the example reports the mean and standard deviation accuracy of the model.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

In this case, we can see the random subspace ensemble with default hyperparameters achieves a classification accuracy of about 85.4 percent on this test dataset.

Mean Accuracy: 0.854 (0.039)

We can also use the random subspace ensemble model as a final model and make predictions for classification.

First, the ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.

The example below demonstrates this on our binary classification dataset.

# make predictions using random subspace ensemble via bagging for classification
from sklearn.datasets import make_classification
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier(bootstrap=False, max_features=10)
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[-4.7705504,-1.88685058,-0.96057964,2.53850317,-6.5843005,3.45711663,-7.46225013,2.01338213,-0.45086384,-1.89314931,-2.90675203,-0.21214568,-0.9623956,3.93862591,0.06276375,0.33964269,4.0835676,1.31423977,-2.17983117,3.1047287]]
yhat = model.predict(row)
print('Predicted Class: %d' % yhat[0])

Running the example fits the random subspace ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.

Predicted Class: 1

Now that we are familiar with using bagging for classification, let’s look at the API for regression.

Random Subspace Ensemble for Regression

In this section, we will look at using bagging for a regression problem.

First, we can use the make_regression() function to create a synthetic regression problem with 1,000 examples and 20 input features.

The complete example is listed below.

# test regression dataset
from sklearn.datasets import make_regression
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5)
# summarize the dataset
print(X.shape, y.shape)

Running the example creates the dataset and summarizes the shape of the input and output components.

(1000, 20) (1000,)

Next, we can evaluate a random subspace ensemble via bagging on this dataset.

As before, we must configure bagging to use all rows of the training dataset and specify the number of input features to randomly select.

...
# define the model
model = BaggingRegressor(bootstrap=False, max_features=10)

As we did with the last section, we will evaluate the model using repeated k-fold cross-validation, with three repeats and 10 folds. We will report the mean absolute error (MAE) of the model across all repeats and folds. The scikit-learn library makes the MAE negative so that it is maximized instead of minimized. This means that larger negative MAE are better and a perfect model has a MAE of 0.

The complete example is listed below.

# evaluate random subspace ensemble via bagging for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.ensemble import BaggingRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5)
# define the model
model = BaggingRegressor(bootstrap=False, max_features=10)
# define the evaluation procedure
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model
n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

Running the example reports the mean and standard deviation accuracy of the model.

In this case, we can see that the bagging ensemble with default hyperparameters achieves a MAE of about 114.

MAE: -114.630 (10.920)

We can also use the random subspace ensemble model as a final model and make predictions for regression.

First, the ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.

The example below demonstrates this on our regression dataset.

# random subspace ensemble via bagging for making predictions for regression
from sklearn.datasets import make_regression
from sklearn.ensemble import BaggingRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5)
# define the model
model = BaggingRegressor(bootstrap=False, max_features=10)
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[0.88950817,-0.93540416,0.08392824,0.26438806,-0.52828711,-1.21102238,-0.4499934,1.47392391,-0.19737726,-0.22252503,0.02307668,0.26953276,0.03572757,-0.51606983,-0.39937452,1.8121736,-0.00775917,-0.02514283,-0.76089365,1.58692212]]
yhat = model.predict(row)
print('Prediction: %d' % yhat[0])

Running the example fits the random subspace ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.

Prediction: -157

Now that we are familiar with using the scikit-learn API to evaluate and use random subspace ensembles, let’s look at configuring the model.

Random Subspace Ensemble Hyperparameters

In this section, we will take a closer look at some of the hyperparameters you should consider tuning for the random subspace ensemble and their effect on model performance.

Explore Number of Trees

An important hyperparameter for the random subspace method is the number of decision trees used in the ensemble. More trees will stabilize the variance of the model, countering the effect of the number of features selected by each tree that introduces diversity.

The number of trees can be set via the “n_estimators” argument and defaults to 10.

The example below explores the effect of the number of trees with values between 10 to 5,000.

# explore random subspace ensemble number of trees effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	n_trees = [10, 50, 100, 500, 1000, 5000]
	for n in n_trees:
		models[str(n)] = BaggingClassifier(n_estimators=n, bootstrap=False, max_features=10)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model):
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	scores = evaluate_model(model)
	results.append(scores)
	names.append(name)
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

Running the example first reports the mean accuracy for each configured number of decision trees.

In this case, we can see that that performance appears to continue to improve as the number of ensemble members is increased to 5,000.

>10 0.853 (0.030)
>50 0.885 (0.038)
>100 0.891 (0.034)
>500 0.894 (0.036)
>1000 0.894 (0.034)
>5000 0.896 (0.033)

A box and whisker plot is created for the distribution of accuracy scores for each configured number of trees.

We can see the general trend of further improvement with the number of decision trees used in the ensemble.

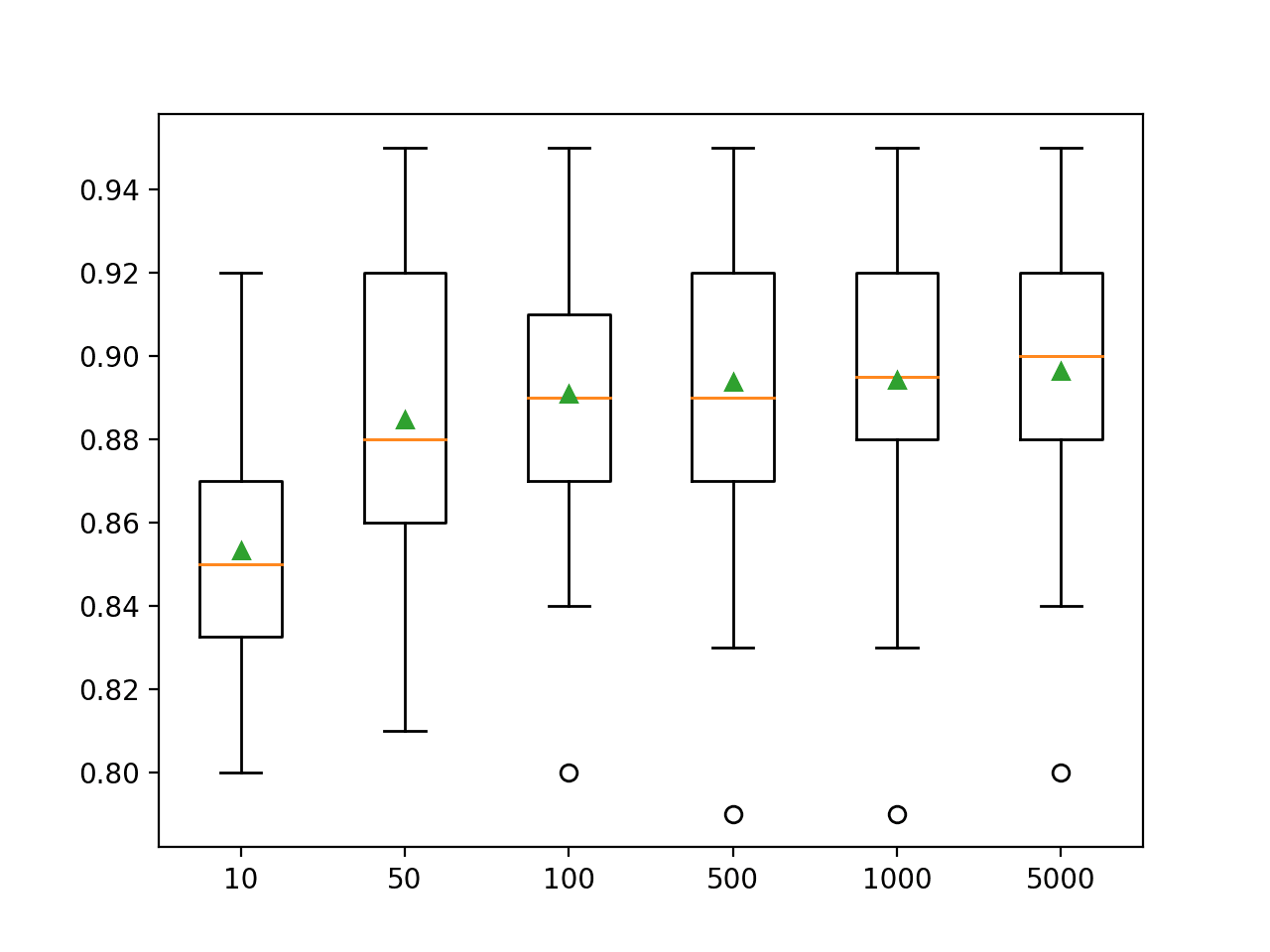
Box Plot of Random Subspace Ensemble Size vs. Classification Accuracy

Explore Number of Features

The number of features selected for each random subspace controls the diversity of the ensemble.

Fewer features mean more diversity, whereas more features mean less diversity. More diversity may require more trees to reduce the variance of predictions made by the model.

We can vary the diversity of the ensemble by varying the number of random features selected by setting the “max_features” argument.

The example below varies the value from 1 to 20 with a fixed number of trees in the ensemble.

# explore random subspace ensemble number of features effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	for n in range(1,21):
		models[str(n)] = BaggingClassifier(n_estimators=100, bootstrap=False, max_features=n)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model):
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	scores = evaluate_model(model)
	results.append(scores)
	names.append(name)
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

Running the example first reports the mean accuracy for each number of features.

In this case, we can see that perhaps using 8 to 11 features in the random subspaces might be appropriate on this dataset when using 100 decision trees. This might suggest increasing the number of trees to a large value first, then tuning the number of features selected in each subset.

>1 0.607 (0.036)
>2 0.771 (0.042)
>3 0.837 (0.036)
>4 0.858 (0.037)
>5 0.869 (0.034)
>6 0.883 (0.033)
>7 0.887 (0.038)
>8 0.894 (0.035)
>9 0.893 (0.035)
>10 0.885 (0.038)
>11 0.892 (0.034)
>12 0.883 (0.036)
>13 0.881 (0.044)
>14 0.875 (0.038)
>15 0.869 (0.041)
>16 0.861 (0.044)
>17 0.851 (0.041)
>18 0.831 (0.046)
>19 0.815 (0.046)
>20 0.801 (0.049)

A box and whisker plot is created for the distribution of accuracy scores for each number of random subset features.

We can see a general trend of increasing accuracy to a point and a steady decrease in performance after 11 features.

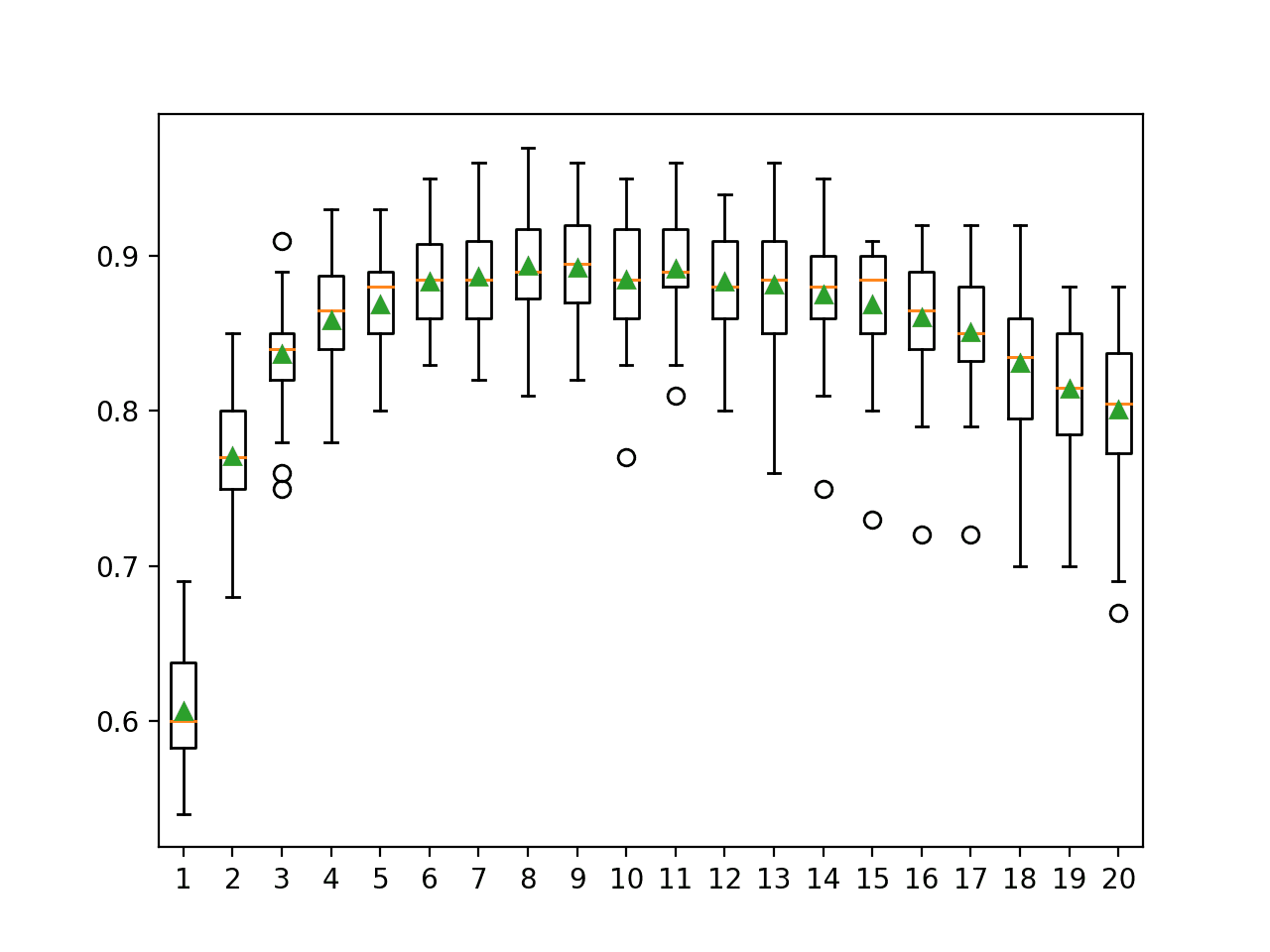
Box Plot of Random Subspace Ensemble Features vs. Classification Accuracy

Explore Alternate Algorithm

Decision trees are the most common algorithm used in a random subspace ensemble.

The reason for this is that they are easy to configure and work well on most problems.

Other algorithms can be used to construct random subspaces and must be configured to have a modestly high variance. One example is the k-nearest neighbors algorithm where the k value can be set to a low value.

The algorithm used in the ensemble is specified via the “base_estimator” argument and must be set to an instance of the algorithm and algorithm configuration to use.

The example below demonstrates using a KNeighborsClassifier as the base algorithm used in the random subspace ensemble via the bagging class. Here, the algorithm is used with default hyperparameters where k is set to 5.

...
# define the model
model = BaggingClassifier(base_estimator=KNeighborsClassifier(), bootstrap=False, max_features=10)

The complete example is listed below.

# evaluate random subspace ensemble with knn algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier(base_estimator=KNeighborsClassifier(), bootstrap=False, max_features=10)
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

Running the example reports the mean and standard deviation accuracy of the model.

In this case, we can see the random subspace ensemble with KNN and default hyperparameters achieves a classification accuracy of about 90 percent on this test dataset.

Accuracy: 0.901 (0.032)

Summary

In this tutorial, you discovered how to develop random subspace ensembles for classification and regression.

Specifically, you learned:

Random subspace ensembles are created from decision trees fit on different samples of features (columns) in the training dataset.
How to use the random subspace ensemble for classification and regression with scikit-learn.
How to explore the effect of random subspace model hyperparameters on model performance.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

The post How to Develop a Random Subspace Ensemble With Python appeared first on Machine Learning Mastery.

Go to Source

How to Develop a Random Subspace Ensemble With Python

Tutorial Overview

Random Subspace Ensemble

Random Subspace Ensemble via Bagging

Random Subspace Ensemble for Classification

Random Subspace Ensemble for Regression

Random Subspace Ensemble Hyperparameters

Explore Number of Trees

Explore Number of Features

Explore Alternate Algorithm

Further Reading

Papers

Books

APIs

Articles

Summary